Librosa处理音频信号

二十世纪八十年代，有专家研究巴赫《第一勃兰登堡协奏曲》的音乐信号时发现，音乐信号的功率谱与人类大脑生理信号的功率谱相似，符合1/f信号公式。还发现，音乐信号α越靠近数值1越好听，从科学上找到一个近似参数来判定音乐的悦耳度。2012年加拿大麦吉尔大学音乐系主任分析发现，音乐节奏也满足这个规律，α值为0.8。不同音乐体裁的α值不一样，所以也可以用这个数值反推音乐的风格体裁。不同作曲家风格音乐的α值不一样，但是作曲家们所作出来的各种风格体裁的音乐的参数是相似的。在本文中，我们将研究如何用Python处理音频/音乐信号，再利用所学的技能将音乐片段分类为不同的类型。

使用Python进行音频处理

声音以具有诸如频率、带宽、分贝等参数的音频信号的形式表示，典型的音频信号可以表示为幅度和时间的函数。

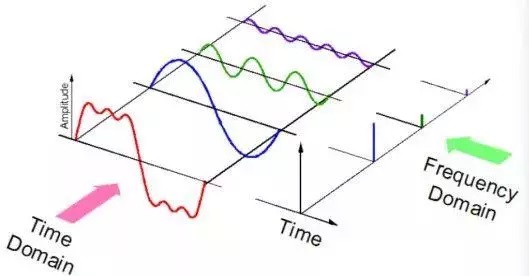
这些声音有多种格式，使计算机可以读取和分析它们。例如：

• mp3格式
• wma（Windows Media Audio）格式
• wav（波形音频文件）格式

音频库

Python有一些很棒的音频处理库，比如Librosa和PyAudio。还有一些内置的模块用于一些基本的音频功能。

我们将主要使用两个库进行音频采集和回放：

1. Librosa

它是一个Python模块，通常用于分析音频信号，但更倾向于音乐。它包括用于构建MIR（音乐信息检索）系统的nuts 和 bolts。示例和教程：https://librosa.github.io/librosa/

安装

pip install librosa
# or
conda install -c conda-forge librosa

为了提供更多的音频解码能力，您可以安装随许多音频解码器一起提供的ffmpeg。

2. IPython.display.Audio

IPython.display.Audio 让您直接在jupyter笔记本中播放音频。

加载音频文件

import librosa

audio_path = '../T08-violin.wav'
x , sr = librosa.load(audio_path)
print(type(x), type(sr))
# <class 'numpy.ndarray'> <class 'int'>
print(x.shape, sr)
# (396688,) 22050

这会将音频时间序列作为numpy数组返回，默认采样率（sr）为22KHZ mono。我们可以通过以下方式更改此行为：

librosa.load(audio_path, sr=44100)

以44.1KHz重新采样，或禁用重新采样。采样率是每秒传输的音频样本数，以Hz或kHz为单位。

librosa.load(audio_path, sr=None)

播放音频

使用IPython.display.Audio播放音频。

import IPython.display as ipd
ipd.Audio(audio_path)

然后返回jupyter笔记本中的音频小部件，如下图所示，这个小部件在这里不起作用，但它可以在你的笔记本中使用，你甚至可以使用mp3或WMA格式作为音频示例。

可视化音频

波形

我们可以绘制音频数组librosa.display.waveplot：

import matplotlib.pyplot as plt
import librosa.display

plt.figure(figsize=(14, 5))
librosa.display.waveplot(x, sr=sr)

这里，我们有波形幅度包络图(amplitude envelope):

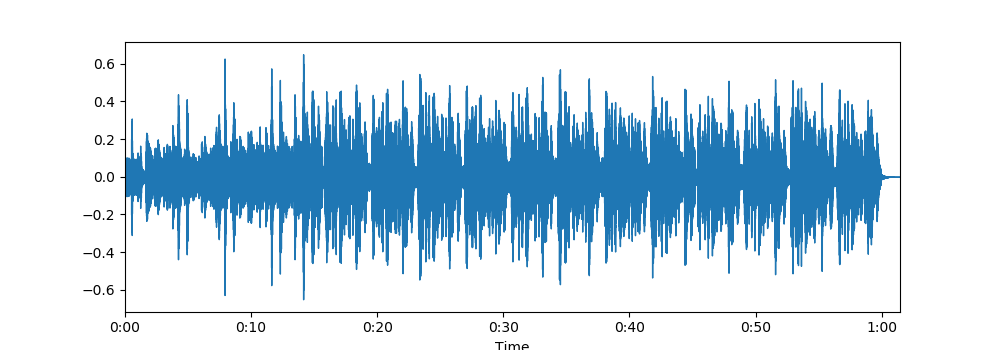
声谱图(spectrogram)

声谱图（spectrogram）是声音或其他信号的频率随时间变化时的频谱（spectrum）的一种直观表示。声谱图有时也称sonographs,voiceprints,或者voicegrams。当数据以三维图形表示时，可称其为瀑布图（waterfalls）。在二维数组中，第一个轴是频率，第二个轴是时间。

我们可以使用显示频谱图： librosa.display.specshow.

X = librosa.stft(x)
Xdb = librosa.amplitude_to_db(abs(X))
plt.figure(figsize=(14, 5))
librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='hz')
plt.colorbar()

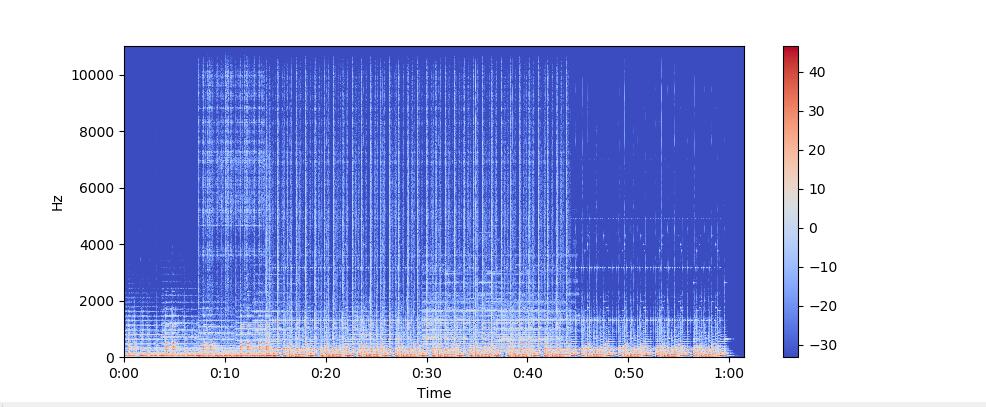
纵轴表示频率（从0到10kHz），横轴表示剪辑的时间。由于我们看到所有动作都发生在频谱的底部，我们可以将频率轴转换为对数轴。

librosa.display.specshow(Xdb, sr=sr, x_axis='time', y_axis='log')
plt.colorbar()

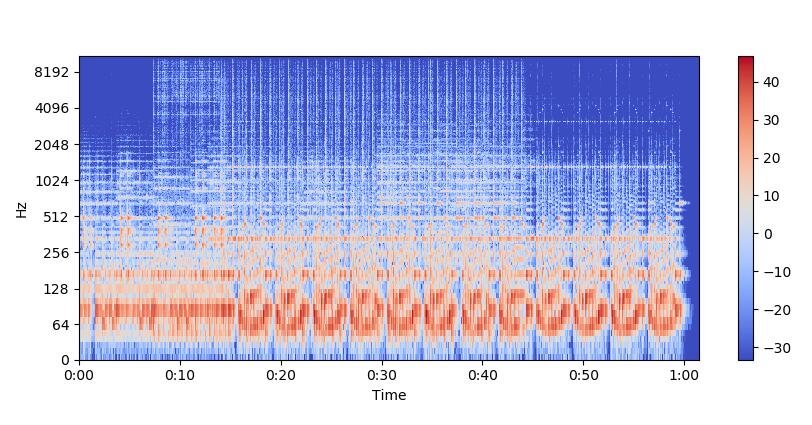
写音频

librosa.output.write_wav 将NumPy数组保存到WAV文件。

librosa.output.write_wav('example.wav', x, sr)

创建音频信号

现在让我们创建一个220Hz的音频信号，音频信号是一个numpy数组，所以我们将创建一个并将其传递给音频函数。

import numpy as np
sr = 22050 # sample rate
T = 5.0    # seconds
t = np.linspace(0, T, int(T*sr), endpoint=False) # time variable
x = 0.5*np.sin(2*np.pi*220*t)# pure sine wave at 220 Hz
Playing the audio
ipd.Audio(x, rate=sr) # load a NumPy array
Saving the audio
librosa.output.write_wav('tone_220.wav', x, sr)

特征提取

每个音频信号都包含许多特征。但是，我们必须提取与我们试图解决的问题相关的特征。提取要使用它们进行分析的特征的过程称为特征提取，让我们详细研究一些特征。

我们将提取以下特征：
• 过零率 Zero Crossing Rate
• 频谱质心 Spectral Centroid
• 声谱衰减 Spectral Roll-off
• 梅尔频率倒谱系数 Mel-frequency cepstral coefficients (MFCC)
• 色度频率 Chroma Frequencies

过零率 Zero Crossing Rate

过零率（zero crossing rate）是一个信号符号变化的比率，即，在每帧中，语音信号从正变为负或从负变为正的次数。这个特征已在语音识别和音乐信息检索领域得到广泛使用，通常对类似金属、摇滚等高冲击性的声音的具有更高的价值。

该特征在语音识别和音乐信息检索中都被大量使用。对于像金属和岩石那样的高冲击声，它通常具有更高的值。让我们计算示例音频片段的过零率。

# Load the signal
x, sr = librosa.load('../T08-violin.wav')
#Plot the signal:
plt.figure(figsize=(14, 5))
librosa.display.waveplot(x, sr=sr)
# Zooming in
n0 = 9000
n1 = 9100
plt.figure(figsize=(14, 5))
plt.plot(x[n0:n1])
plt.grid()

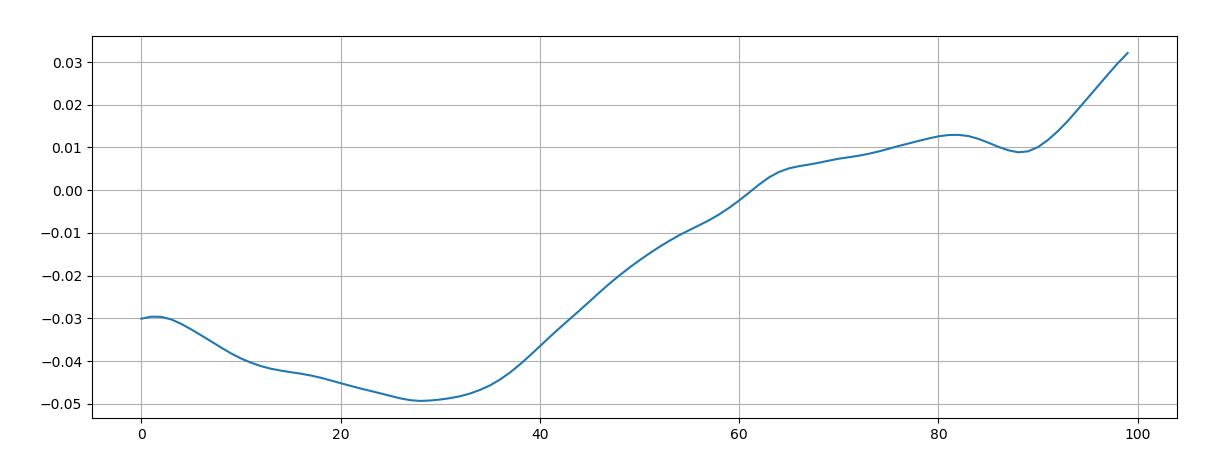
似乎有1个过零点，让我们用librosa验证。

zero_crossings = librosa.zero_crossings(x[n0:n1], pad=False)
print(sum(zero_crossings))

光谱质心 Spectral Centroid

频谱质心(Spectral Centroid)指示声音的“质心”位于何处，并按照声音的频率的加权平均值来加以计算。假设现有两首歌曲，一首是蓝调歌曲，另一首是金属歌曲。现在，与同等长度的蓝调歌曲相比，金属歌曲在接近尾声位置的频率更高。所以蓝调歌曲的频谱质心会在频谱偏中间的位置，而金属歌曲的频谱质心则靠近频谱末端。

librosa.feature.spectral_centroid 计算信号中每帧的光谱质心：

spectral_centroids = librosa.feature.spectral_centroid(x, sr=sr)[0]
print(spectral_centroids.shape)
# (2647,)
# Computing the time variable for visualization
frames = range(len(spectral_centroids))
t = librosa.frames_to_time(frames)
# Normalising the spectral centroid for visualisation
def normalize(x, axis=0):
    return sklearn.preprocessing.minmax_scale(x, axis=axis)
#Plotting the Spectral Centroid along the waveform
librosa.display.waveplot(x, sr=sr, alpha=0.4)
plt.plot(t, normalize(spectral_centroids), color='r')

到最后，光谱质心上升。

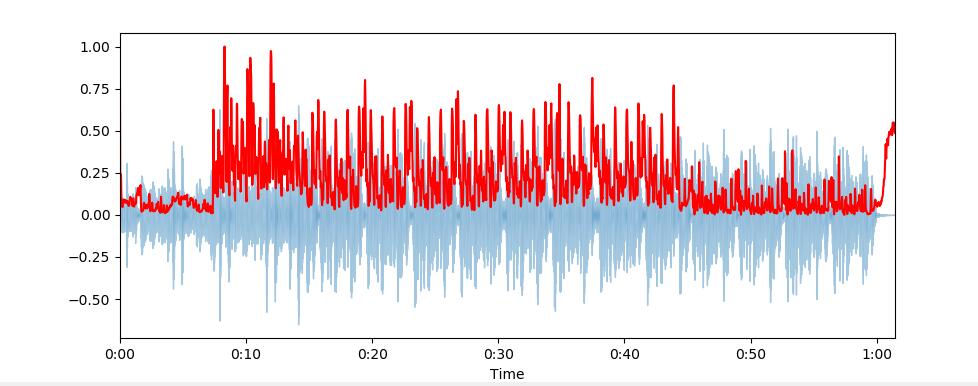
声谱衰减 Spectral Roll-off

它是信号形状的度量。librosa.feature.spectral_rolloff 计算信号中每帧的滚降系数：

spectral_rolloff = librosa.feature.spectral_rolloff(x+0.01, sr=sr)[0]
librosa.display.waveplot(x, sr=sr, alpha=0.4)
plt.plot(t, normalize(spectral_rolloff), color='r')

梅尔频率倒谱系数 MFCC

信号的Mel频率倒谱系数（MFCC）是一小组特征（通常约10-20），其简明地描述了频谱包络的整体形状，它模拟了人声的特征。让我们这次用一个简单的循环波。

mfccs = librosa.feature.mfcc(x, sr=fs)
print mfccs.shape
# (20, 97)
#Displaying  the MFCCs:
librosa.display.specshow(mfccs, sr=sr, x_axis='time')

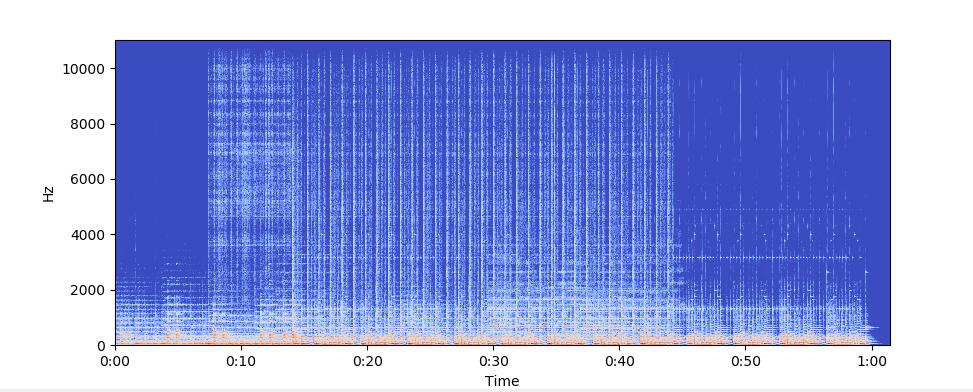
这里mfcc计算了超过97帧的20个MFCC。我们还可以执行特征缩放，使得每个系数维度具有零均值和单位方差：

import sklearn
mfccs = sklearn.preprocessing.scale(mfccs, axis=1)
print(mfccs.mean(axis=1))
print(mfccs.var(axis=1))
librosa.display.specshow(mfccs, sr=sr, x_axis='time')

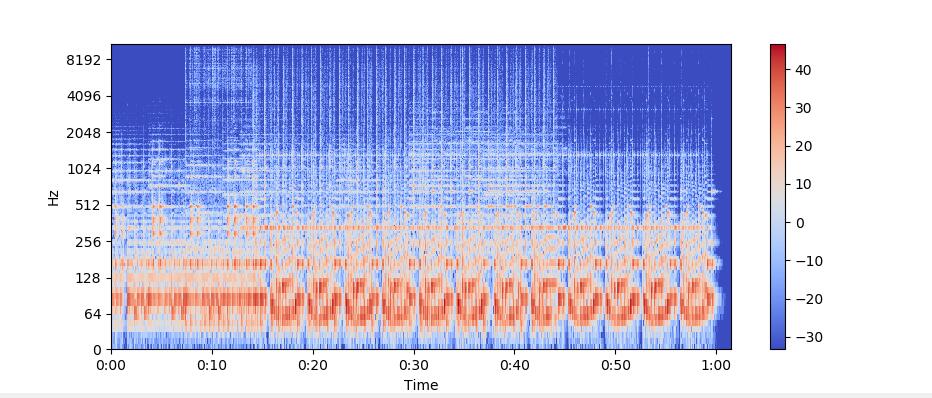
色度频率 Chroma Frequencies

色度频率是音乐音频有趣且强大的表示，其中整个频谱被投影到12个区间，代表音乐八度音的12个不同的半音（或色度），librosa.feature.chroma_stft 用于计算。

x, sr = librosa.load('../simple_piano.wav')
hop_length = 512
chromagram = librosa.feature.chroma_stft(x, sr=sr, hop_length=hop_length)
plt.figure(figsize=(15, 5))
librosa.display.specshow(chromagram, x_axis='time', y_axis='chroma', hop_length=hop_length, cmap='coolwarm')

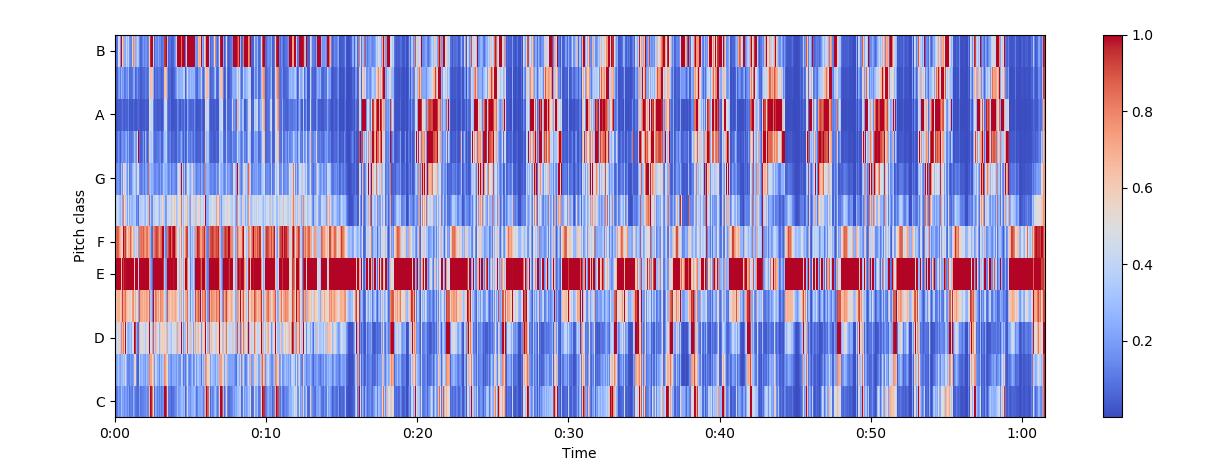
音频预处理

Dynamic range compression

动态范围压缩（DRC）或简单地压缩为一个音频信号处理操作，降低响亮的体积声音或放大安静的声音从而减少或压缩的音频信号的动态范围。压缩通常用于声音的记录和再现，广播，[1] 现场声音增强和某些乐器放大器中。

def dynamic_range_compression(x, C=1, clip_val=1e-5):
    return torch.log(torch.clamp(x, min=clip_val) * C)

原始音频：

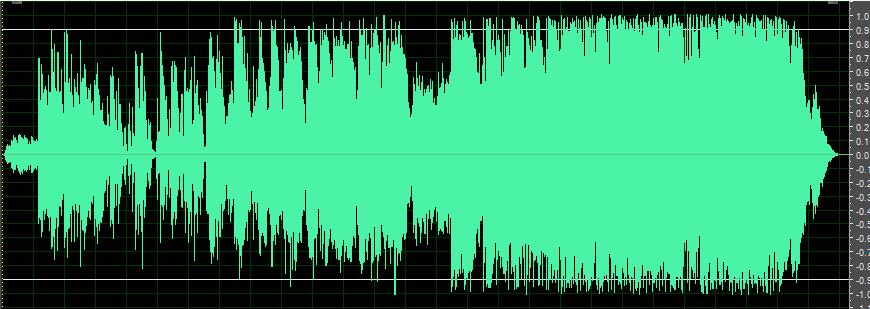
放大二倍后的波形：

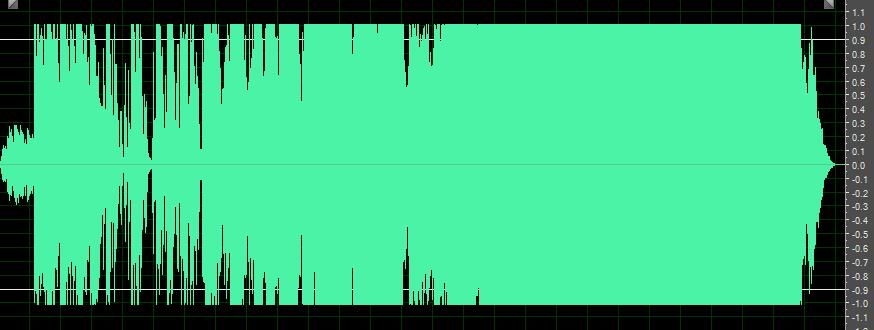
放大二倍后经过DRC(简单点说，大值小倍数变化，小值正常倍数变化，之前处理爆音时，本能的就使用过这个思想，没想到这玩意专业术语叫做DRC)处理，防止爆音后的波形。

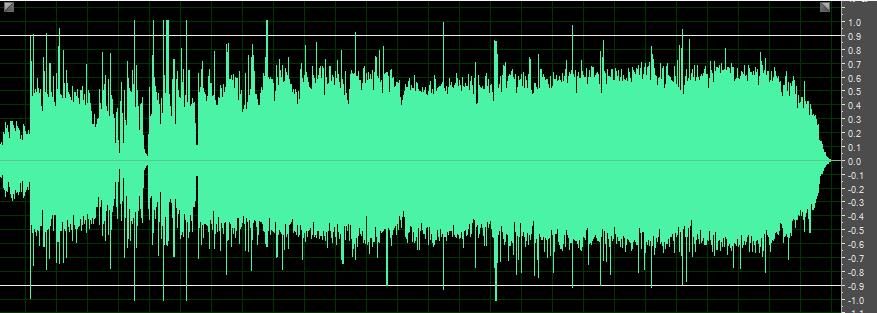
API 附录

短时傅里叶变换

librosa.stft(y, n_fft=2048, 
            hop_length=None, 
            win_length=None, 
            window='hann', 
            center=True, 
            pad_mode='reflect')

短时傅立叶变换（STFT），返回一个复数矩阵使得D(f,t)

复数的实部：np.abs(D(f,t))频率的振幅
复数的虚部：np.angle(D(f,t))频率的相位

参数：

• y：音频时间序列
• n_fft：FFT窗口大小，n_fft=hop_length+overlapping
• hop_length：帧移，如果未指定，则默认win_length / 4
• win_length：每一帧音频都由window()加窗。窗长win_length，然后用零填充以匹配n_fft
默认win_length=n_fft。
• window：字符串，元组，数字，函数 shape =（n_fft, )
窗口（字符串，元组或数字）
窗函数，例如scipy.signal.hanning
长度为n_fft的向量或数组
• center：bool
如果为True，则填充信号y，以使帧 D [:, t]以y [t * hop_length]为中心
如果为False，则D [:, t]从y [t * hop_length]开始
• dtype：D的复数值类型。默认值为64-bit complex复数
• pad_mode：如果center = True，则在信号的边缘使用填充模式
默认情况下，STFT使用reflection padding

• STFT矩阵 $ shape =（1 + \frac{n-fft}{2}，t）$

短时傅里叶逆变换

librosa.istft(stft_matrix, 
        hop_length=None, 
        win_length=None, 
        window='hann', 
        center=True, 
        length=None)

短时傅立叶逆变换(ISTFT), 将复数值D(f,t)频谱矩阵转换为时间序列y，窗函数、帧移等参数应与stft相同

参数：

• stft_matrix ：经过STFT之后的矩阵
• hop_length ：帧移，默认为winlength4
• win_length ：窗长，默认为n_fft
• window：字符串，元组，数字，函数或shape = (n_fft, )
窗口（字符串，元组或数字）
窗函数，例如scipy.signal.hanning
长度为n_fft的向量或数组
• center：bool
如果为True，则假定D具有居中的帧
如果False，则假定D具有左对齐的帧
• length：如果提供，则输出y为零填充或剪裁为精确长度音频

• y ：时域信号

幅度转dB

librosa.amplitude_to_db(S, ref=1.0)

将幅度频谱转换为dB标度频谱。也就是对S取对数。与这个函数相反的是librosa.db_to_amplitude(S)

参数：

• S ：输入幅度
• ref ：参考值，振幅abs（S）相对于ref进行缩放，20∗log10(Sref)

• dB为单位的S

功率转dB

librosa.core.power_to_db(S, ref=1.0)

将功率谱（幅度平方）转换为分贝（dB）单位，与这个函数相反的是librosa.db_to_power(S)

参数：

• S：输入功率
• ref ：参考值，振幅abs(S)相对于ref进行缩放，10∗log10(Sref)

• dB为单位的S

Mel滤波器组

librosa.filters.mel(sr, n_fft, n_mels=128, fmin=0.0, fmax=None, htk=False, norm=1)

创建一个滤波器组矩阵以将FFT合并成Mel频率

参数：

• sr ：输入信号的采样率
• n_fft ：FFT组件数
• n_mels ：产生的梅尔带数
• fmin ：最低频率（Hz）
• fmax：最高频率（以Hz为单位）。如果为None，则使用fmax = sr / 2.0
• norm：{None，1，np.inf} [标量]
如果为1，则将三角mel权重除以mel带的宽度（区域归一化）否则，保留所有三角形的峰值为1.0

• Mel变换矩阵

提取MFCC系数

MFCC特征是一种在自动语音识别和说话人识别中广泛使用的特征。关于MFCC特征的详细信息，有兴趣的可以参考博客。在librosa中，提取MFCC特征只需要一个函数：

librosa.feature.mfcc(y=None, 
        sr=22050, 
        S=None, 
        n_mfcc=20, 
        dct_type=2, 
        norm='ortho', 
        **kwargs)

参数：

• y：音频数据
• sr：采样率
• S：np.ndarray，对数功能梅尔谱图
• n_mfcc：int>0，要返回的MFCC数量
• dct_type：None, or {1, 2, 3} 离散余弦变换（DCT）类型。默认情况下，使用DCT类型2。
• norm： None or ‘ortho’ 规范。如果dct_type为2或3，则设置norm =’ortho’使用正交DCT基础
标准化不支持dct_type = 1。

• M： MFCC序列

Home

Librosa处理音频信号

使用Python进行音频处理

音频库

1. Librosa

安装

2. IPython.display.Audio

播放音频

可视化音频

波形

声谱图(spectrogram)

写音频

创建音频信号

特征提取

过零率 Zero Crossing Rate

光谱质心 Spectral Centroid

声谱衰减 Spectral Roll-off

梅尔频率倒谱系数 MFCC

色度频率 Chroma Frequencies

音频预处理

Dynamic range compression

API 附录

短时傅里叶变换

参数：

返回：

短时傅里叶逆变换

参数：

返回：

幅度转dB

参数：

返回：

功率转dB

参数：

返回：

Mel滤波器组

参数：

返回：

提取MFCC系数

参数：

返回：