文字转语音TTS

概述

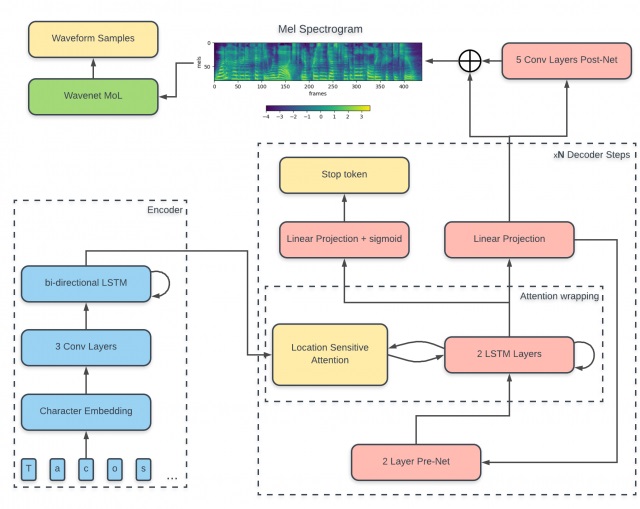
Tacotron2是由Google Brain 2017年提出来的一个语音合成框架Tacotron2:一个完整神经网络语音合成方法。模型主要由三部分组成：
• 声谱预测网络：一个引入注意力机制（attention）的基于循环的Seq2seq的特征预测网络，用于从输入的字符序列预测梅尔频谱的帧序列。
• 声码器（vocoder）：一个WaveNet的修订版，用预测的梅尔频谱帧序列来生成时域波形样本。
• 中间连接层：使用低层次的声学表征-梅尔频率声谱图来衔接系统的两个部分。

预处理

文字处理

一般传给模型的编码好的词向量，而不是原始的文字，因此我们需要对文字进行编码,压缩到一个固定长度的向量。文字主要由字幕和标点、空格等组成，这里先将文字转换成对应的向量，如果是汉字的话，可以先转成拼音。步骤如下：

先清除文字里陌生字符，可以使用正则表达式匹配
```
_curly_re = re.compile(r'(.*?)\{(.+?)\}(.*)')
```

对每个字母进行编码, 得到一个词向量，然后传给模型

 _pad = '_'
 _punctuation = '!\'(),.:;? '
 _special = '-'
 _letters = 'ABCDEFGHIJKLMNOPQRSTUVWXYZabcdefghijklmnopqrstuvwxyz'

 # Prepend "@" to ARPAbet symbols to ensure uniqueness:
 _arpabet = ['@' + s for s in cmudict.valid_symbols]

 # Export all symbols:
 symbols = [_pad] + list(_special) + list(_punctuation) + list(_letters) + _arpabet

 def sequence_to_text(sequence):
     result = ''
     for symbol_id in sequence:
         if symbol_id in _id_to_symbol:
             s = _id_to_symbol[symbol_id]
             if len(s) > 1 and s[0] == '@':
                 s =  s[1:]
             result += s
     return result.replace('}{', ' ')

声音处理

一般很难直接能从声音的波形图里，提取出声音的特征，需要先进行转换。一般的话，都是转换为梅尔图谱或者梅尔频率倒谱系数 MFCC，在谷歌的论文里转换成了梅尔图谱。

使用librosa或者scipy.io.wavfile 加载到内存，得到numpy array

from scipy.io.wavfile import read
sampling_rate, data = read(full_path)

进行加窗、短时傅里叶变换进入复数域

from scipy.signal import get_window

# get window and zero center pad it to filter_length
fft_window = get_window(window, win_length, fftbins=True)
fft_window = pad_center(fft_window, filter_length)
fft_window = torch.from_numpy(fft_window).float()
forward_basis *= fft_window
inverse_basis *= fft_window
# 加窗
forward_transform = F.conv1d(
        input_data,
        Variable(self.forward_basis, requires_grad=False),
        stride=self.hop_length, padding=0)
# 短时傅里叶变换       
cutoff = int((self.filter_length / 2) + 1)
real_part = forward_transform[:, :cutoff, :]  # 实部
imag_part = forward_transform[:, cutoff:, :]  # 虚部
magnitude = torch.sqrt(real_part ** 2 + imag_part ** 2)
mel_output = torch.matmul(self.mel_basis, magnitudes)

傅里叶变换

上述处理声音用到短时傅里叶变换，如果已经对傅里叶变换了解可以跳过此小节。

傅立叶变换，表示能将满足一定条件的某个函数表示成三角函数（正弦和/或余弦函数）或者它们的积分的线性组合。在不同的研究领域，傅立叶变换具有多种不同的变体形式，如连续傅立叶变换和离散傅立叶变换。

傅里叶变换把时域信号变为频域信号。在离散傅里叶变换中，频域信号由一系列不同频率的谐波（频率成倍数）组成。scipy.fftpack.fft返回值是一个复数数组，每个复数表示一个正弦波。通常一个波形由振幅，相位，频率三个变量确定，可以从fft的返回值里，获取这些信息。

假设a是时域中的周期信号，采样频率为Fs，采样点数为N。如果A[N] = fft(a[N])，返回值A[N]是一个复数数组，其中：

• A[0]表示频率为0hz的信号，即直流分量

• A[1:N/2]包含正频率项，A[N/2:]包含负频率项。正频率项就是转化后的频域信号，通常我们只需要正频率项，即前面的n/2项，负频率项是计算的中间结果（正频率项的镜像值）

• A[i] = real + j * imag，是一个复数，相位就是复数的辐角，相位 = arg(real/imag)

• 振幅就是复数的模，振幅 = $\sqrt{real^2+imag^2}$。但是fft的返回值的模是放大值，直流分量的振幅放大了N倍，弦波分量的振幅放大了N/2倍

import numpy as np
from scipy.fftpack import fft, ifft
import matplotlib.pyplot as plt

x = np.linspace(0, 1, 800)

# 设置需要采样的信号，频率分量有80，190和300
y = 7 * np.sin(2 * np.pi * 80 * x) + \
    2.8 * np.sin(2 * np.pi * 190 * x) + \
    5.1 * np.sin(2 * np.pi * 300 * x)

yy = fft(y)  # 快速傅里叶变换
y_real = yy.real  # 获取实数部分
y_imag = yy.imag  # 获取虚数部分

yf = abs(fft(y))  # 取绝对值
yf1 = 2 * abs(fft(y)) / len(x)  # 归一化处理
yf2 = yf1[range(int(len(x) / 2))]  # 由于对称性，只取一半区间

xf = np.arange(len(y))  # 频率
xf1 = xf
xf2 = xf[range(int(len(x) / 2))]  # 取一半区间

plt.figure(figsize=(10, 4))
plt.subplot(231)
plt.plot(x[0:50], y[0:50])

plt.subplot(232)
plt.plot(xf, y_real, 'r')

plt.subplot(233)
plt.plot(xf, y_imag, 'g')

plt.subplot(234)
plt.plot(xf1, yf, 'g')

plt.subplot(235)
plt.plot(xf1, yf1, 'r')

plt.subplot(236)
plt.plot(xf2, yf2, 'b')

plt.show()

代码来源gist, 运行效果如下：

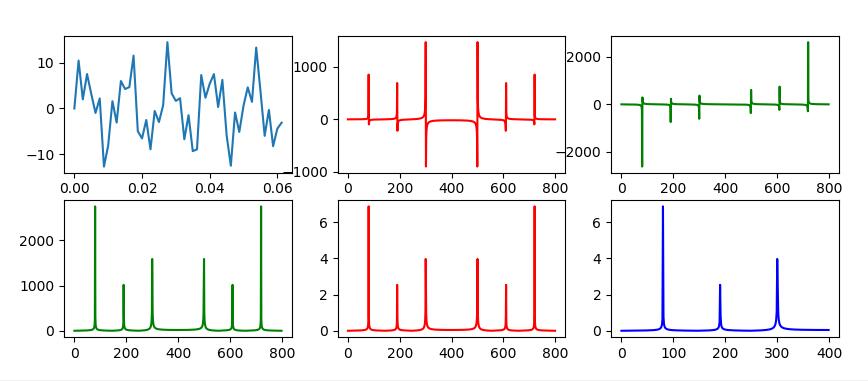
(Fig1原始波形，Fig2实数部分, Fig3虚数部分，Fig4绝对值, Fig5归一化，Fig6对称取半)

从上图可以清晰看到傅里叶变换之后，频域对称性分布(傅立叶变换的共轭对称性)，归一化之后得到每一个频率的振幅。

STFT

短时傅里叶变换（STFT，short-time Fourier transform，或 short-term Fourier transform)）是和傅里叶变换相关的一种数学变换，用以确定时变信号其局部区域正弦波的频率与相位。

选择一个时频局部化的窗函数，假定分析窗函数g(t)在一个短时间间隔内是平稳（伪平稳）的，移动窗函数，使f(t)g(t)在不同的有限时间宽度内是平稳信号，从而计算出各个不同时刻的功率谱。短时傅里叶变换使用一个固定的窗函数，窗函数一旦确定了以后，其形状就不再发生改变，短时傅里叶变换的分辨率也就确定了。如果要改变分辨率，则需要重新选择窗函数。短时傅里叶变换用来分析分段平稳信号或者近似平稳信号犹可，但是对于非平稳信号，当信号变化剧烈时，要求窗函数有较高的时间分辨率；而波形变化比较平缓的时刻，主要是低频信号，则要求窗函数有较高的频率分辨率。

DCT

由于许多要处理的信号都是实信号，在使用FFT时，对于实信号，傅立叶变换的共轭对称性导致在频域中有一半的数据冗余。

离散余弦变换（DCT）是对实信号定义的一种变换，变换后在频域中得到的也是一个实信号，相比离散傅里叶变换DFT而言, DCT可以减少一半以上的计算。DCT还有一个很重要的性质（能量集中特性）：大多书自然信号（声音、图像）的能量都集中在离散余弦变换后的低频部分，因而DCT在（声音、图像）数据压缩中得到了广泛的使用。由于DCT是从DFT推导出来的另一种变换，因此许多DFT的属性在DCT中仍然是保留下来的。

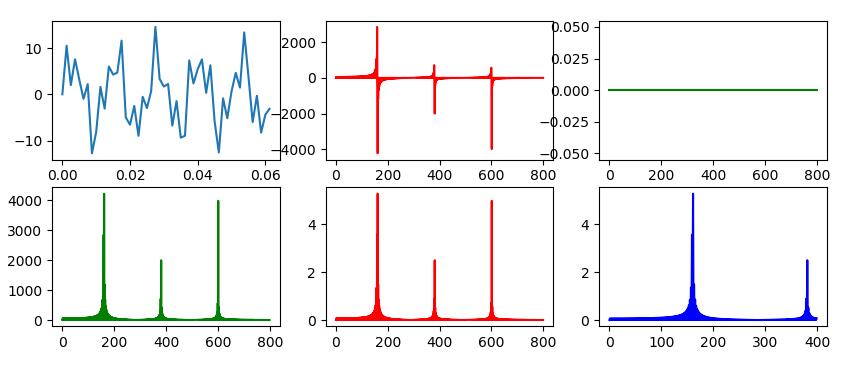
SciPy.fftpack中，提供了离散余弦变换(DCT)与离散余弦逆变换(IDCT)的实现。我们将上面fft运算改成dct运算，
修改后的代码运行效果如下:

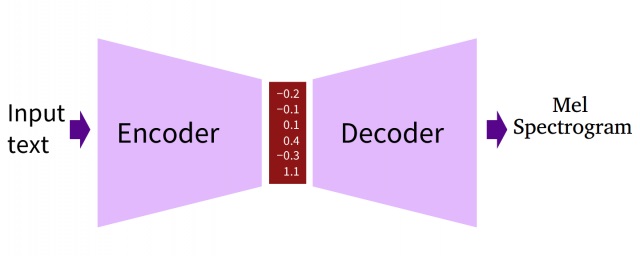
编码器-解码器(Encoder-Decoder)结构

在原始的编码器-解码器结构中，编码器(encoder)输入一个序列或句子，然后将其压缩到一个固定长度的向量(向量也可以理解为一种形式的序列)中；解码器(decoder)使用固定长度的向量，将其解压成一个序列。

最普遍的方式是使用RNN实现编码器和解码器。

编码器将输入序列映射成固定长度的向量，解码器在生成输出序列阶段，利用注意力机制“关注”向量的不同部分。

编码器

前置知识

双向RNN

双向RNN确保模型能够同时感知前向和后向的信息。双向RNN包含两个独立的RNN，一个前向RNN从前向后读入序列(从$f_1$到$f_{Tx}$)，另一个后向RNN从后向前读入序列(从$f_{Tx}$到$f_1$)，最终的输出为两者的拼接。

在Tacotron2中，编码器将输入序列$X=[x_1,x_2,…,x_{T_x}]$映射成序列$H=[h_1,h_2,…,h_{T_x}]$,其中序列H被称作“编码器隐状态”(encoder hidden states)。注意：编码器的输入输出序列都拥有相同的长度，$h_i$之于相邻分量$h_j$拥有的信息等价于$x_i$之于$x_j$所拥有的信息。

在Tacotron2中，每一个输入分量$x_i$就是一个字符。Tacotron2的编码器是一个3层卷积层后跟一个双向LSTM层形成的模块，在Tacotron2中卷积层给予了神经网络类似于N−gram感知上下文的能力。这里使用卷积层获取上下文主要是由于实践中RNN很难捕获长时依赖，并且卷积层的使用使得模型对不发音字符更为鲁棒(如’know’中的’k’)。

经词嵌入(word embedding)的字符序列先送入三层卷积层以提取上下文信息，然后送入一个双向的LSTM中生成编码器隐状态，即：

$f_{e}=ReLU(F_3*ReLU(F_2*ReLU(F_1*\overline{E}(X))))\\ H=EncoderRecurrency(f_{e})$

其中，F1、F2、F3为3个卷积核，ReLU为每一个卷积层上的非线性激活，$\overline{E}$表示对字符序列X做embedding，EncoderRecurrency表示双向LSTM。

编码器隐状态生成后，就会将其送入注意力网络(attention network)中生成上下文向量(context vector)。

注意力机制

注意力(attention)用作编码器和解码器的桥接，本质是一个上下文权重向量组成的矩阵。

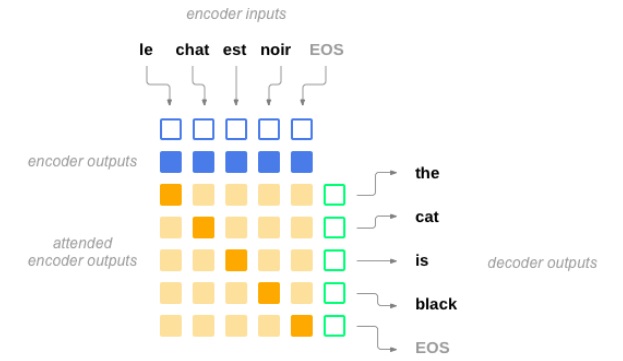
$Attention(Query,Source)=\sum_{i=1}^{L_x}similarity(Query,Key_i)*Value$

如果在机器翻译(NMT)中，Souce中的Key和Value合二为一，指的是同一个东西，即输入句子中每个单词对应的语义编码。

一般的计算步骤：

步骤一：Key和Value相似度度量：

• 点积 $Similarity(Query,Key)=Query·Key$
• cos相似性 $Similarity(Query,Key)=\frac{Query·Key_i}{||Query||*||Key_i||}$
• MLP网络 $Similarity(Query,Key_i)=MLP(Query,Key_i)$
• Key和Value还可以拼接后再内积一个参数向量，甚至权重都不一定要归一化

步骤二：softmax归一化(alignments/attention weights):

$a_i=softmax(sim_i)=\frac{e^{sim_i}}{\sum_{j=1}^{L_x}e^{sim_j}}$

步骤三：Attention数值(context vector)：

$Attention(Query,Key)=\sum^{L_x}_{i=1}a_i·Value_i$

在Tacotron中，注意力计算(attention computation)发生在每一个解码器时间步上，其包含以下阶段：

目标隐状态(上图绿框所示)与每一个源状态(上图蓝框所示)“相比”，以生成注意力权重(attention weights)或称对齐(alignments)：

其中，$h_t$为目标隐状态，$\overline{h_s}$为源状态，score函数常被称作“能量”(energy)，因此可以表示为e。不同的score函数决定了不同类型的注意力机制。

基于注意力权重，计算上下文向量(context vector)作为源状态的加权平均：

$c_t=\sum_s\alpha_{ts}\overline{h_s}$

注意力向量作为下一个时间步的输入

以下是不同的score函数：

基于内容的注意力机制(content-based attention)：

$e_{ij}=score(s_{i-1},h_j)=v_a^Ttanh(W_as_{i-1}+U_ah_j)$

其中，$s_{i−1}$为上一个时间步中解码器的输出(解码器隐状态，decoder hidden states)，$h_j$是编码器此刻输入(编码器隐状态，encoder hidden state j)，$v_a$、$W_a$和$U_a$是待训练参数张量。由于$U_ah_j$是独立于解码步i的，因此可以独立提前计算。基于内容的注意力机制能够将不同的输出与相应的输入元素连接，而与其位置无关。在Tacotron2中使用基于内容的注意力机制时，当输出对应于’s’的Mel频谱帧，模型会寻找所有所有对应于’s’的输入。

基于位置的注意力机制(location-based attention)：

$e_{ij}=score(\alpha_{i-1},h_j)=v_a^Ttanh(Wh_j+Uf_{i,j})$

其中，$f_{i,j}$是之前的注意力权重αi−1经卷积而得的位置特征，$f_i=F∗\alpha_{i−1}$，$v_a$、$W_a$、$U_a$和F是待训练参数。

基于位置的注意力机制仅关心序列元素的位置和它们之间的距离。基于位置的注意力机制会忽略静音或减少它们，因为该注意力机制没有发现输入的内容。

混合注意力机制(hybrid attention)：

顾名思义，混合注意力机制是上述两者注意力机制的结合：

$e_{ij}=score(s_{i-1},\alpha_{i-1},h_j)=v_a^T\mathop{tanh}(Ws_{i-1}+Vh_j+Uf_{i,j})$

其中，$s_{i−1}$为之前的解码器隐状态，$\alpha_{i−1}$是之前的注意力权重，$h_j$是第j个编码器隐状态。为其添加偏置值b，最终的score函数计算如下：

其中，$v_a$、W、V、U和b为待训练参数，$s_{i−1}$为上一个时间步中解码器隐状态，$h_j$是当前编码器隐状态，$f_{i,j}$是之前的注意力权重$α_{i−1}$经卷积而得的位置特征(location feature)， $f_i=F∗\alpha_{i−1}$。混合注意力机制能够同时考虑内容和输入元素的位置。

Tacotron2注意力机制，Location Sensitive Attention

$e_{i,j}=score(s_i,c\alpha_{i-1},h_j)=v_a^T\mathop{tanh}(Ws_i+Vh_j+Uf_{i,j}+b)$

其中，$s_i$为当前解码器隐状态而非上一步解码器隐状态，偏置值b被初始化为0。位置特征$f_i$使用累加注意力权重$c\alpha_i$卷积而来：

$f_i=F*c\alpha_{i-1}\\ c\alpha_i=\sum_{j=1}^{i-1}\alpha_j$

之所以使用加法累加而非乘法累积，原因如图：

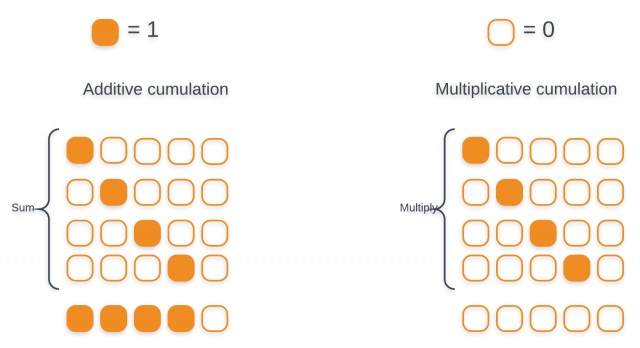
累加注意力权重，可以使得注意力权重网络了解它已经学习到的注意力信息，使得模型能在序列中持续进行并且避免重复未预料的语音。

整个注意力机制如图：

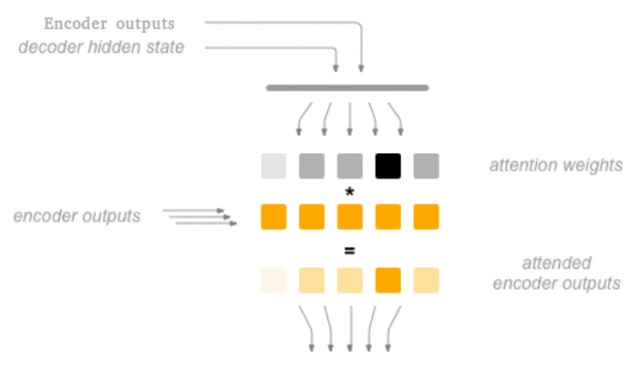
解码器

解码过程从输入上一步的输出声谱或上一步的真实声谱到PreNet开始，解码过程如图：

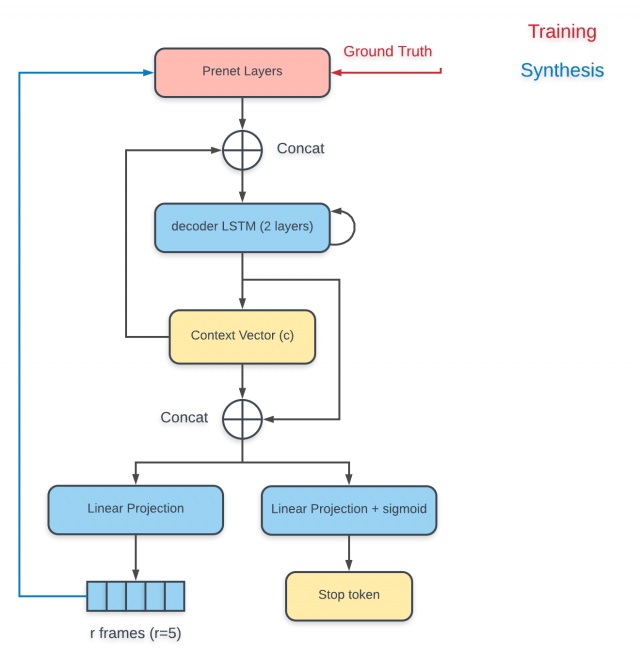
PreNet的输出与使用上一个解码步输出计算而得的上下文向量做拼接，然后整个送入RNN解码器中，RNN解码器的输出用来计算新的上下文向量，最后新计算出来的上下文向量与解码器输出做拼接，送入投影层(projection layer)以预测输出。输出有两种形式，一种是声谱帧，一种是的概率，后者是一个简单二分类问题，决定解码过程是否结束。使用缩减因子(reduction factor)即每一个解码步仅允许预测r(缩减因子)Mel谱帧，能够有效加速计算，减小内存占用。

后处理网络

一旦解码器完成解码，预测得到的Mel谱被送入一系列的卷积层中以提高生成质量。

后处理网络使用残差(residual)计算：

$y_{final}=y+y_r$

其中，y为原始输入

上式中，

$y_r=PostNet(y)=W_{ps}f_{ps}+b_{ps}$

其中，$f_{ps}=F_{ps,i}*x$，x为上一个卷积层的输出或解码器输出，F为卷积

训练

$loss=\frac{1}{n}\sum_{i=1}^{n}(y_{real,i}-y_i)^2+\frac{1}{n}\sum_{i=1}^n(y_{real,i}-y_{final,i})^2+\lambda\sum_{j=1}^p w_j^2$

其中，$y_{real}$,i为真实声谱，$y_i$、$y_{final}$,i分别为进入后处理网络前、后的声谱，n为batch中的样本数，λ为正则化参数，p为参数总数，w为神经网络中的参数。注意，不需要正则化偏置值。