图形噪声
大自然蕴含着各式各样的纹理,小到细胞菌落分布,大到宇宙星球表面。运用图形噪声,我们可以在3d场景中模拟它们,本文就带大家一起走进万能的图形噪声。 图形噪声,是计算机图形学中一类随机算法,经常用来模拟自然界中的各种纹理材质,如下图的云、山脉等,都是通过噪声算法模拟出来的。

通过不同的噪声算法,作用在物体纹理和材质细节,我们可以模拟不同类型的材质。

基础噪声算法
一个基础的噪声函数的入参通常是一个点坐标(这个点坐标可以是二维的、三维的,甚至N维),返回值是一个浮点数值:noise(vec2(x,y))。
我们将这个浮点值转成灰度颜色,形成噪声图,具体可以通过编写片元着色器程序来绘制。

上图是各类噪声函数在片元着色器中的运行效果,代码如下:
// noise fragment shader
varying vec2 uv;
float noise(vec2 p) {
// TODO
}
void main() {
float n = noise(uv); // 通过噪声函数计算片元坐标对应噪声值
gl_FragColor = vec4(n, n, n, 1.0);
}
其中noise(uv)的入参uv是片元坐标,返回的噪声值映射在片元的颜色上。
目前基础噪声算法比较主流的有两类:1. 梯度噪声;2. 细胞噪声;
梯度噪声 (Gradient Noise)
梯度噪声产生的纹理具有连续性,所以经常用来模拟山脉、云朵等具有连续性的物质,该类噪声的典型代表是Perlin Noise。

其它梯度噪声还有Simplex Noise和Wavelet Noise,它们也是由Perlin Noise演变而来。
算法步骤
梯度噪声是通过多个随机梯度相互影响计算得到,通过梯度向量的方向与片元的位置计算噪声值。这里以2d举例,主要分为四步:1. 网格生成;2. 网格随机梯度生成;3. 梯度贡献值计算;4. 平滑插值
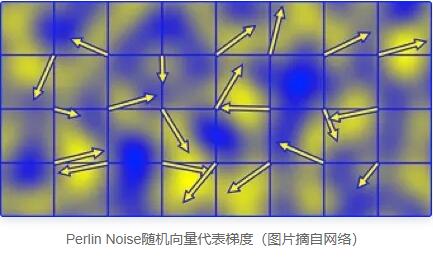
第一步,我们将2d平面分成m×n个大小相同的网格,具体数值取决于我们需要生成的纹理密度(下面以4×4作为例子);
#define SCALE 4. // 将平面分为 4 × 4 个正方形网格
float noise(vec2 p) {
p *= SCALE;
// TODO
}
第二步,梯度向量生成,这一步是根据第一步生成的网格的顶点来产生随机向量,四个顶点就有四个梯度向量;
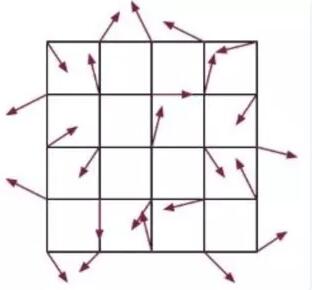
我们需要将每个网格对应的随机向量记录下来,确保不同片元在相同网格中获取的随机向量是一致的。
// 输入网格顶点位置,输出随机向量
vec2 random(vec2 p){
return -1.0 + 2.0 * fract(
sin(
vec2(
dot(p, vec2(127.1,311.7)),
dot(p, vec2(269.5,183.3))
)
) * 43758.5453
);
}
如上,借用三角函数sin(θ)的来生成随机值,入参是网格顶点的坐标,返回值是随机向量。
第三步,梯度贡献计算,这一步是通过计算四个梯度向量对当前片元点P的影响,主要先求出点P到四个顶点的距离向量,然后和对应的梯度向量进行点积。
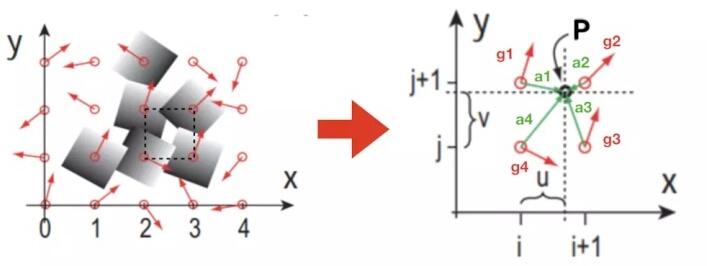
如图,网格内的片元点P的四个顶点距离向量为a1, a2, a3, a4,此时将距离向量与梯度向量g1, g2, g3, g4进行点积运算:c[i] = a[i] · g[i];
第四步,平滑插值,这一步我们对四个贡献值进行线性叠加,使用smoothstep()方法,平滑网格边界,最终得到当前片元的噪声值。具体代码如下:
float noise_perlin (vec2 p) {
vec2 i = floor(p); // 获取当前网格索引i
vec2 f = fract(p); // 获取当前片元在网格内的相对位置
// 计算梯度贡献值
float a = dot(random(i),f); // 梯度向量与距离向量点积运算
float b = dot(random(i + vec2(1., 0.)),f - vec2(1., 0.));
float c = dot(random(i + vec2(0., 1.)),f - vec2(0., 1.));
float d = dot(random(i + vec2(1., 1.)),f - vec2(1., 1.));
// 平滑插值
vec2 u = smoothstep(0.,1.,f);
// 叠加四个梯度贡献值
return mix(mix(a,b,u.x),mix(c,d,u.x),u.y);
}
Perlin-Noise-Texture的生成代码我已上传ShaderToy, 预览如下(国内加载有点儿慢)。
细胞噪声 (Celluar Noise)

Celluar Noise生成的噪声图由很多个“晶胞”组成,每个晶胞向外扩张,晶胞之间相互抑制。这类噪声可以模拟细胞形态、皮革纹理等。

算法步骤
细胞噪声算法主要通过距离场的形式实现的,以单个特征点为中心的径向渐变,多个特征点共同作用而成。主要分为三步:1. 网格生成;2. 特征点生成;3. 最近特征点计算
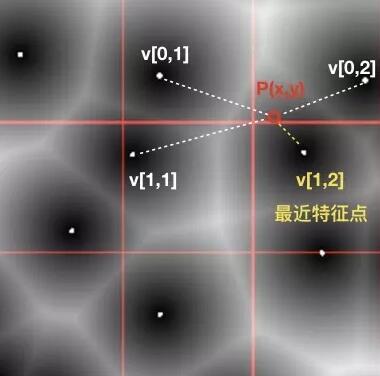
第一步,网格生成:将平面划分为m×n个网格,这一步和梯度噪声的第一步一样;
第二步,特征点生成:为每个网格分配一个特征点v[i,j],这个特征点的位置在网格内随机。
// 输入网格索引,输出网格特征点坐标
vec2 random(vec2 st){
return fract(
sin(
vec2(
dot(st, vec2(127.1,311.7)),
dot(st, vec2(269.5,183.3))
)
) * 43758.5453
);
}
第三步,针对当前像素点p,计算出距离点p最近的特征点v,将点p到点v的距离记为F1;
float noise(vec2 p) {
vec2 i = floor(p); // 获取当前网格索引i
vec2 f = fract(p); // 获取当前片元在网格内的相对位置
float F1 = 1.;
// 遍历当前像素点相邻的9个网格特征点
for (int j = -1; j <= 1; j++) {
for (int k = -1; k <= 1; k++) {
vec2 neighbor = vec2(float(j), float(k));
vec2 point = random(i + neighbor);
float d = length(point + neighbor - f);
F1 = min(F1,d);
}
}
return F1;
}
求解F1,我们可以遍历所有特征点v,计算每个特征点v到点p的距离,再取出最小的距离F1;但实际上,我们只需遍历离点p最近的网格特征点即可。在2d中,则最多遍历包括自身相连的9个网格,如图:
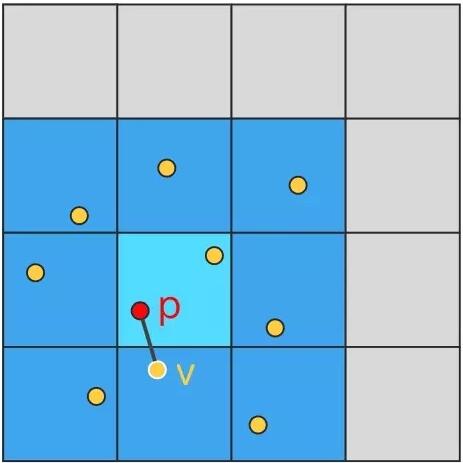
最后一步,将F1映射为当前像素点的颜色值,可以是gl_FragColor = vec4(vec3(pow(noise(uv), 2.)), 1.0);。
不仅如此,我们还可以取特征点v到点p第二近的距离F2,通过F2 - F1,得到类似泰森多变形的纹理,如上图最右侧。
Celluar Noise Texture 生成算法我已经上传ShaderToy, 预览如下 (国内加载有点慢):
噪声算法组合
前面介绍了两种主流的基础噪声算法,我们可以通过对多个不同频率的同类噪声进行运算,产生更为自然的效果,下图是经过分形操作后的噪声纹理。
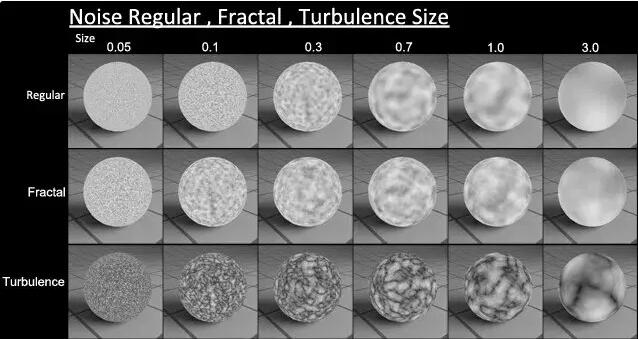
分形布朗运动(Fractal Brownian Motion)
分形布朗运动,简称fbm,是通过将不同频率和振幅的噪声函数进行操作,最常用的方法是:将频率乘2的倍数,振幅除2的倍数,线性相加。

公式:fbm = noise(st) + 0.5 * noise(2*st) + 0.25 * noise(4*st)
// fragment shader片元着色器
#define OCTAVE_NUM 5
// 叠加5次的分形噪声
float fbm_noise(vec2 p)
{
float f = 0.0;
p = p * 4.0;
float a = 1.;
for (int i = 0; i < OCTAVE_NUM; i++)
{
f += a * noise(p);
p = 4.0 * p;
a /= 4.;
}
return f;
}
基于 PerlinNoise 的fbm算法在 ShaderToy 中预览如下 (国内加载有点慢):
湍流(Turbulence)
另外一种变种是在fbm中对噪声函数取绝对值,使噪声值等于0处发生突变,产生湍流纹理:
公式:fbm = |noise(st)| + 0.5 * |noise(2*st)| + 0.25 * |noise(4*st)|
// 湍流分形噪声
float fbm_abs_noise(vec2 p)
{
...
for (int i = 0; i < OCTAVE_NUM; i++)
{
f += a * abs(noise(p)); // 对噪声函数取绝对值
...
}
return f;
}
基于 PerlinNoise 的Turbulence算法在 ShaderToy 中预览如下 (国内加载有点慢):
翘曲域(Domain Wrapping)

翘曲域噪声用来模拟卷曲、螺旋状的纹理,比如烟雾、大理石等,实现公式如下:
对于图像定义为函数f(x,y), 更紧凑地写为f(p),其中p是空间中的位置,我们可以据此评估定义(等)表面或图像颜色的体积密度。弯曲只是意味着我们在评估f之前用另一个函数g(p)扭曲域。基本上,我们将f(p)替换为f(g(p))。g可以是任何东西,有意义的是让g(p)就是恒等式加上一个小的任意失真h(p), 即:
这种技术非常强大,可让您塑造苹果,建筑物,动物或您可能想象的其他任何东西。 我们针对f和h使用基于fBM, 产生一些抽象但美丽的图像,并具有相当的品相。

我们对初始的fBM公式进行变换:
代码如下:
float pattern( in vec2 p )
{
vec2 q = vec2( fbm( p + vec2(0.0,0.0) ),
fbm( p + vec2(5.2,1.3) ) );
return fbm( p + 4.0*q );
}
进行更复杂的变换:
float pattern( in vec2 p )
{
vec2 q = vec2( fbm( p + vec2(0.0,0.0) ),
fbm( p + vec2(5.2,1.3) ) );
vec2 r = vec2( fbm( p + 4.0*q + vec2(1.7,9.2) ),
fbm( p + 4.0*q + vec2(8.3,2.8) ) );
return fbm( p + 4.0*r );
}
实现效果参考shadertoy的预览(国内加载可能有点儿慢):
动态纹理
前面讲的都是基于2d平面的静态噪声,我们还可以在2d基础上加上时间t维度,形成动态的噪声。
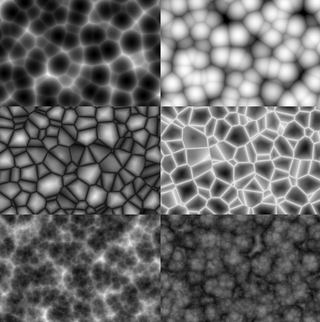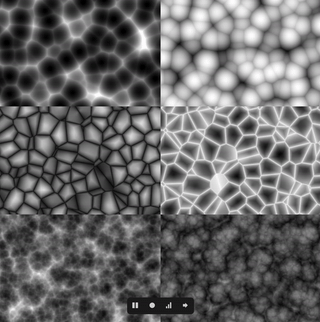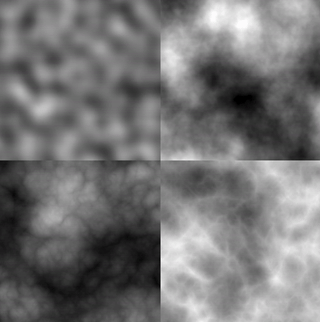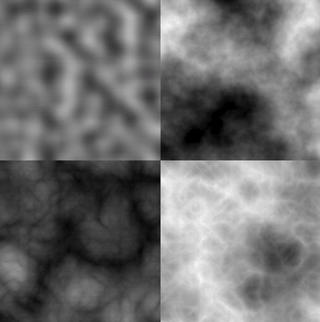
如下为实现3d noise的代码结构:
// noise fragment shader
#define SPEED 20.
varying vec2 uv;
uniform float u_time;
float noise(vec3 p) {
// TODO
}
void main() {
float n = noise(uv, u_time * SPEED); // 传入片元坐标与时间
gl_FragColor = vec4(n, n, n, 1.0);
}
利用时间,我们可以生成实现动态纹理,模拟如火焰、云朵的变换。

噪声贴图应用
利用噪声算法,我们可以构造物体表面的纹理颜色和材质细节,在3d开发中,一般采用贴图方式应用在3D Object上的Material材质上。
Color Mapping
彩色贴图是最常用的是方式,即直接将噪声值映射为片元颜色值,作为材质的Texture图案。

Height Mapping
另一种是作为Height Mapping高度贴图,生成地形高度。高度贴图的每个像素映射到平面点的高度值,通过图形噪声生成的Height Map可模拟连绵起伏的山脉。

Normal Mapping
除了通过heightMap生成地形,还可以通过法线贴图改变光照效果,实现材质表面的凹凸细节。

这里的噪声值被映射为法线贴图的color值。
参考文献:
1、《大自然的分形几何学》[波] 伯努瓦·B. 曼德布罗特(Mandelbrot)
2、Perlin Noise
3、关于噪声的一些基本定义
4、Fractal Brownian Motion
5、Understanding Perlin Noise
6、谈谈噪声
7、基于ComputeShader生成Perlin Noise噪声图
8、Understanding Perlin Noise