TensorFlow 学习入门
TensorFlow是谷歌基于DistBelief进行研发的第二代人工智能学习系统,其命名来源于本身的运行原理。Tensor(张量)意味着N维数组,Flow(流)意味着基于数据流图的计算,TensorFlow为张量从流图的一端流动到另一端计算过程。TensorFlow是将复杂的数据结构传输至人工智能神经网中进行分析和处理过程的系统。
导入TensorFlow
典型的导入TensorFlow程序的做法如下:
import tensorflow as tf运行这个,可以得到Python下的TensorFlow中的所有类、方法和符号。大多数的文档默认你已经执行了这个。
计算图 (Computational Graph)
TensorFlow Core程序是由两个分离的部分组成的:
1、构建计算图。
2、运行计算图。
一个计算图是一系列TensorFlow操作的点(nodes)。我们构建一个简单的计算图。每一个点需要零个或者更多的张量(tensor)作为输入,并且产生一个张量作为输出。
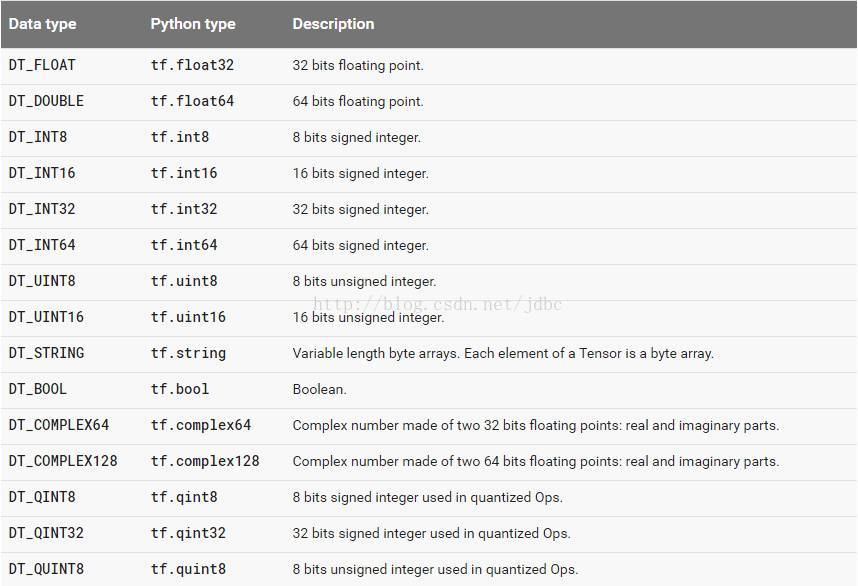
数据类型
下图列出了所有的 tensorflow的数据类型
常量(Constant)
点的一种形式是常数。像所有TensorFlow常数,它不需要输入,而它会从内部输出一个值。我们可以创建两个点的张量c1和c2,如下所示:
import tensorflow as tf
import numpy as np
c1 = tf.constant([0.3,2.0],tf.float32)
c2 = tf.constant([1.3,1.2],tf.float32)
print c1,c2
"""
输出:Tensor("Const:0", shape=(2,), dtype=float32) Tensor("Const_1:0", shape=(2,), dtype=float32)
"""注意到,它输出的并不是[0.3,2.0]和([1.3,1.2]的值,而是对应的点张量,要通过开启会话,才能直接输出其值。这直接反映了TensorFlow的构建和计算是分离的。
张量的阶、形状
TensorFlow用张量这种数据结构来表示所有的数据.你可以把一个张量想象成一个n维的数组或列表.一个张量有一个静态类型和动态类型的维数.张量可以在图中的节点之间流通.
阶
在TensorFlow系统中,张量的维数来被描述为阶.但是张量的阶和矩阵的阶并不是同一个概念.张量的阶(有时是关于如顺序或度数或者是n维)是张量维数的一个数量描述.比如,下面的张量(使用Python中list定义的)就是2阶.
t = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]你可以认为一个二阶张量就是我们平常所说的矩阵,一阶张量可以认为是一个向量.对于一个二阶张量你可以用语句t[i, j]来访问其中的任何元素.而对于三阶张量你可以用’t[i, j, k]’来访问其中的任何元素.
阶 数学实例 Python 例子
0 纯量 (只有大小) s = 483
1 向量(大小和方向) v = [1.1, 2.2, 3.3]
2 矩阵(数据表) m = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
3 3阶张量 (数据立体) t = [[[2], [4], [6]], [[8], [10], [12]], [[14], [16], [18]]]
n n阶 (自己想想看) ….
shape [2,3] 表示为数组的意思是第一维有两个元素,第二维有三个元素,如: [[1,2,3],[4,5,6]]
# 2-D tensor `a`
a = tf.constant([1, 2, 3, 4, 5, 6], shape=[2, 3]) => [[1. 2. 3.]
[4. 5. 6.]]
# 2-D tensor `b`
b = tf.constant([7, 8, 9, 10, 11, 12], shape=[3, 2]) => [[7. 8.]
[9. 10.]
[11. 12.]]
c = tf.matmul(a, b) => [[58 64]
[139 154]]
# 3-D tensor `a`
a = tf.constant(np.arange(1,13), shape=[2, 2, 3]) => [[[ 1. 2. 3.]
[ 4. 5. 6.]],
[[ 7. 8. 9.]
[10. 11. 12.]]]
# 3-D tensor `b`
b = tf.constant(np.arange(13,25), shape=[2, 3, 2]) => [[[13. 14.]
[15. 16.]
[17. 18.]],
[[19. 20.]
[21. 22.]
[23. 24.]]]
c = tf.matmul(a, b) => [[[ 94 100]
[229 244]],
[[508 532]
[697 730]]]tensorflow中有一类在tensor的某一维度上求值的函数,如:
求最大值tf.reduce_max(input_tensor, reduction_indices=None, keep_dims=False, name=None)
求平均值tf.reduce_mean(input_tensor, reduction_indices=None, keep_dims=False, name=None)
参数(1)input_tensor:待求值的tensor。
参数(2)reduction_indices:在哪一维上求解。
参数(3)(4)可忽略
举例说明:
import numpy as np
import tensorflow as tf
x=[[1.,2.],[3.,4.]]
x_=tf.constant(x,shape=[2,2])
with tf.Session() as sess:
y1_ = tf.reduce_mean(x_)
y2_ =tf.reduce_mean(x_,0)
y3_=tf.reduce_mean(x_,1)
print sess.run(y1_),sess.run(y2_),sess.run(y3_)
y1_=tf.reduce_max(x_)
y2_=tf.reduce_max(x_,0)
y3_=tf.reduce_max(x_,1)
print sess.run(y1_),sess.run(y2_),sess.run(y3_)首先求平均值,
tf.reduce_mean(x_) ==> 2.5 #如果不指定第二个参数,那么就在所有的元素中取平均值
tf.reduce_mean(x_, 0) ==> [2., 3.] #指定第二个参数为0,则第一维的元素取平均值,即每一列求平均值
tf.reduce_mean(x_, 1) ==> [1.5, 3.5] #
指定第二个参数为1,则第二维的元素取平均值,即每一行求平均值
同理,还可用tf.reduce_max()求最大值。
#输出结果:
2.5 [2. 3.] [1.5 3.5]
4.0 [3. 4.] [2. 4.]会话
接下来的代码就是创建一个Session对象,调用它的run方法。只有这样,才能进行真正的运算。如下所示:
with tf.Session() as sess:
print sess.run([c1,c2])
# 输出: [array([0.3, 2. ], dtype=float32), array([1.3, 1.2], dtype=float32)]这时,我们就能得到了想象中的两个值。
我们可以通过联合多个张量(Tensors),构建更为复杂的运算。例如,我们可以进行点张量的相加,如下所示:
import tensorflow as tf
import numpy as np
c1 = tf.constant([0.3,2.0],tf.float32)
c2 = tf.constant([1.3,1.2],tf.float32)
op_add = tf.add(c1,c2)
with tf.Session() as sess:
print "op_add rst:{}".format(sess.run(op_add))
# 输出:op_add rst:[1.5999999 3.2 ]占位符(Placeholder)
有些时候,我们不会直接使用常量进行计算,而需要事先创建一个量去表示运算。这时,在TensorFlow中可以采用placeholders的方法。它的本质就是一个占位符,先用placeholder表示进行运算的表达,程序后面在进行“喂值”(feed_dict)。如下所示:
# placeholder
x = tf.placeholder(tf.float32)
y = tf.placeholder(tf.float32)
op_add = tf.add(x,y)由上面操作可见,x和y都没有固定的值,它们创建的目的只是为了表示相加这种运算。
如果程序后面需要用到这种运算,我们可以使用feed_dict进行喂值。
cc =sess.run(op_add,{x:[1.0,2.0,3,4],y:[2,3,4,1]})
print cc
# 输出 [3. 5. 7. 5.]显然,不同的“喂值”,得出的结果可能也不同。
在基础上,我们可以进行更复杂的操作。我们可以对op_add进行相乘操作。如下所示:
c1 = tf.constant(0.3,tf.float32)
c2 = tf.constant(1.3,tf.float32)
op_add = tf.add(c1,c2)
triple=op_add*3
with tf.Session() as sess:
print sess.run([c1,c2])
print "triple rst:{}".format(sess.run(triple))
# 输出:triple rst:4.7999997139当然,要显示最终结果,需要进行回话和喂值。
变量(Variable)
机器学习中,我们构建模型,TensorFlow中模型有输入有输出,训练中参数会不断更新,这时,我们需要创建变量(Variable)。TensorFlow中,Variable可以将训练参数添加到图中,声明变量时,一般需要声明变量的类型(如:tf.float32)和赋初值。如下所示:
x = tf.placeholder(tf.float32)
y = tf.placeholder(tf.float32)
op_add = tf.add(x,y)
op_tri = op_add*3这样,我们就成功地创建了变量。从上面例子,我们可以看出placeholder和Variable的区别。当该量是通过训练更新的,我们可以通过Variable创建,当该量是作为模型的输入,我们可以通过placeholder创建。
当然,变量的启动不仅需要开启会话,还要在会话中进行初始化。
with tf.Session() as sess:
init = tf.global_variables_initializer()
sess.run(init)这样,变量才真正地被初始化。
初始化成功之后,我们给模型喂值,
W = tf.Variable([1.1],tf.float32)
b = tf.Variable([-2.1],tf.float32)
x_train = [1,2,3,4,5,6]
linear_mode=W*x+b
with tf.Session() as sess:
init = tf.global_variables_initializer()
sess.run(init)
print("real vale: {}".format(sess.run(linear_mode,{x:x_train})))其实,这里我们构建了一个很简单的线性模型。我们希望该模型能够进行训练优化,然而,我们没有设定训练集的期望值。因此,我们自定义期望值。
优化训练,我们采用最小二乘法。
代价函数为:cost(x) = sum(linear_model(x) - y)/number of trainset
square_details = tf.square(linear_mode- y)
loss = tf.reduce_sum(square_details)得到了损失函数,我们就可以对模型的准确性进行评估了。
tensorboard
Tensorboard可以记录与展示以下数据形式:
- 标量Scalars
- 图片Images
- 音频Audio
- 计算图Graph
- 数据分布Distribution
- 直方图Histograms
- 嵌入向量Embeddings
Tensorboard的可视化过程
-
首先肯定是先建立一个graph,你想从这个graph中获取某些数据的信息
-
确定要在graph中的哪些节点放置summary operations以记录信息
使用tf.summary.scalar记录标量
常量则可使用Tensorflow.scalar_summary()方法:
tf.scalar_summary(‘loss’,loss) #命名和赋值
使用tf.summary.histogram记录数据的直方图
-
operations并不会去真的执行计算,除非你告诉他们需要去run,或者它被其他的需要run的operation所依赖。而我们上一步创建的这些summary operations其实并不被其他节点依赖,因此,我们需要特地去运行所有的summary节点。但是呢,一份程序下来可能有超多这样的summary 节点,要手动一个一个去启动自然是及其繁琐的,因此我们可以使用tf.summary.merge_all去将所有summary节点合并成一个节点,只要运行这个节点,就能产生所有我们之前设置的summary data。
-
使用tf.summary.FileWriter将运行后输出的数据都保存到本地磁盘中
-
运行整个程序,并在命令行输入运行tensorboard的指令,之后打开web端可查看可视化的结果
#合并到Summary中
merged = tf.merge_all_summaries()
#选定可视化存储目录
writer = tf.train.SummaryWriter("/目录",sess.graph)
#merged也是需要run的
result = sess.run(merged)
writer.add_summary(result,step) 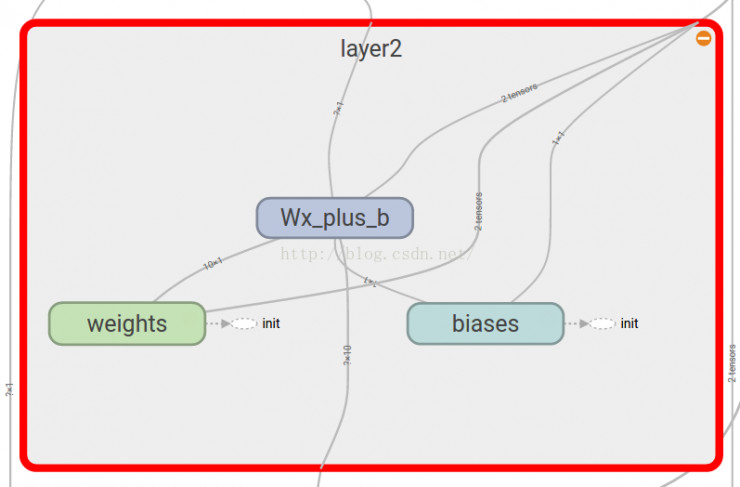
如果6006端口被占用,会报一下错误:
ERROR:tensorflow:Tried to connect to port 6006, but address is in use.
Tried to connect to port 6006, but address is in use.
解决可以使用 –port 指定端口:
tensorboard --host=10.10.101.2 --port=6099 --logdir="my_graph"神经网络
人工神经网络是由大量处理单元互联组成的非线性、自适应信息处理系统。它是在现代神经科学研究成果的基础上提出的,试图通过模拟大脑神经网络处理、记忆信息的方式进行信息处理。
上来先说一个例子。城里正在举办一年一度的游戏动漫展览,小明拿不定主意,周末要不要去参观。
他决定考虑三个因素。
- 天气:周末是否晴天?
- 同伴:能否找到人一起去?
- 价格:门票是否可承受?

现实中,各种因素很少具有同等重要性:某些因素是决定性因素,另一些因素是次要因素。因此,可以给这些因素指定权重(W),代表它们不同的重要性。
权重(W)和阈值(b)
现实中,各种因素很少具有同等重要性:某些因素是决定性因素,另一些因素是次要因素。因此,可以给这些因素指定权重(weight),代表它们不同的重要性。
- 天气:权重为8
- 同伴:权重为4
- 价格:权重为4
这时,还需要指定一个阈值(threshold)。如果总和大于阈值,感知器输出1,否则输出0。假定阈值为8,那么 12 > 8,小明决定去参观。阈值的高低代表了意愿的强烈,阈值越低就表示越想去,越高就越不想去.
决策模型
单个的感知器构成了一个简单的决策模型,已经可以拿来用了。真实世界中,实际的决策模型则要复杂得多,是由多个感知器组成的多层网络。
外部因素 x1、x2、x3 写成矢量 <x1, x2, x3>,简写为 x
权重 w1、w2、w3 也写成矢量 (w1, w2, w3),简写为 w
定义运算 w⋅x = ∑ wx,即 w 和 x 的点运算,等于因素与权重的乘积之和
定义 b 等于负的阈值 b = -threshold
感知器模型就变成了下面这样:
神经网络的运作过程
一个神经网络的搭建,需要满足三个条件。
- 输入和输出
- 权重(w)和阈值(b)
- 多层感知器的结构
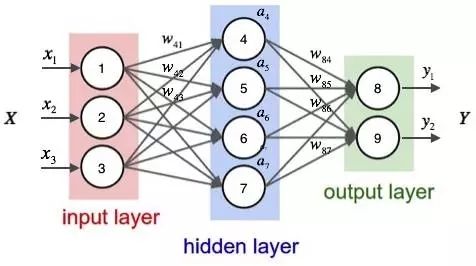
其中,最困难的部分就是确定权重(w)和阈值(b)。目前为止,这两个值都是主观给出的,但现实中很难估计它们的值,必需有一种方法,可以找出答案。
这种方法就是试错法。其他参数都不变,w(或b)的微小变动,记作Δw(或Δb),然后观察输出有什么变化。不断重复这个过程,直至得到对应最精确输出的那组w和b,就是我们要的值。这个过程称为模型的训练。
Tensorflow
求权重和阈值
当然 Google 给了我们一套 api,通过大量的计算,能够得出正确的值。
-
梯度下降算法
梯度下降算法是用的最普遍的优化算法,不过梯度下降算法需要用到全部的样本,训练速度比较慢,但是迭代到一定次数最终能够找到最优解。
tf.train.GradientDescentOptimizer(0.01)
这个类是实现梯度下降算法的优化器,参数learning_rate是要使用的学习率 。详细点击官方API。
-
选择 optimizer 使 loss 达到最小
optimizer.minimize(loss)
我们定义 train 训练模型使损失降到最低,如此反复的训练,求得 权重(w)和阈值(b)的最优解。
就不过多解释了,代码贴出来了:
# -*- coding:utf-8 -*-
import tensorflow as tf
import numpy as np
from board import Board
# 变量
W = tf.Variable([1.1],tf.float32)
b = tf.Variable([-2.1],tf.float32)
# placeholder
x=tf.placeholder(tf.float32)
y=tf.placeholder(tf.float32)
x_train = [1,2,3,4,5,6.1]
y_train = [1,3,5,7,9,11]
feed_dict={x:x_train,y:y_train}
linear_mode=W*x+b
square_details = tf.square(linear_mode - y)
loss = tf.reduce_sum(square_details)
optimizer=tf.train.GradientDescentOptimizer(0.01)
train = optimizer.minimize(loss)
tf.summary.scalar("loss",loss)
merged = tf.summary.merge_all()
with tf.Session() as sess:
summary_writer = tf.summary.FileWriter( "output/",sess.graph)
init = tf.global_variables_initializer()
sess.run(init)
print("real vale: {}".format(sess.run(linear_mode,feed_dict)))
print("curr loss: {}".format(sess.run(loss,feed_dict)))
for i in range(1000):
sess.run(train,feed_dict)
if i % 100 == 0:
cc,res= sess.run([loss,merged],feed_dict)
summary_writer.add_summary(res,i)
print "train step(%s) loss:%s"%(i,cc)
# Evaluate training accuracy
curr_W,curr_b,currr_loss = sess.run([W,b,loss],feed_dict)
print("W: %s,b: %s,loss: %s"%(curr_W,curr_b,currr_loss))
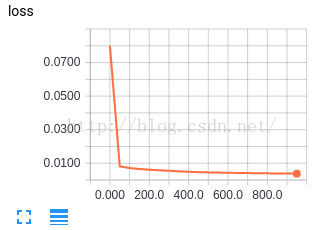
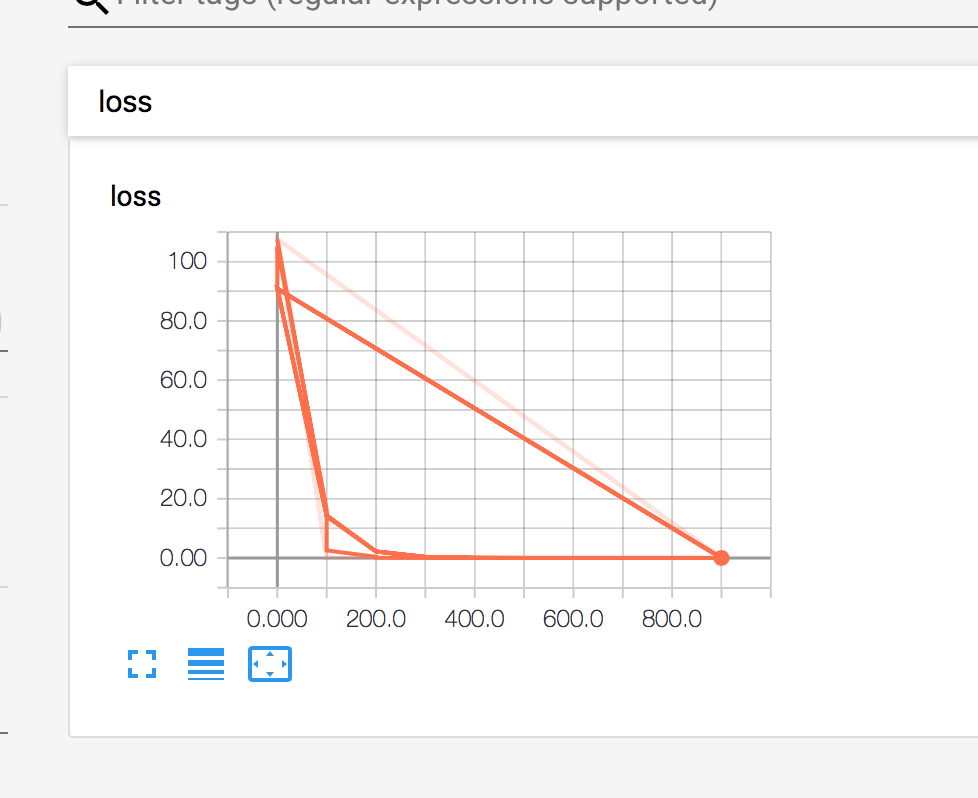
print(sess.run([W,b]))经过1000次训练,我们可以从下图的运行结果可以发现 loss 越来越小了,说明我们的模型值越来越精准。准确率接近100%
最终我们训练出来的模型 W:2.0000005, b:-1.0000029 loss:1.3187673e-11
从 loss 看,训练出来的模型这已经很精准了。
其实作者给出的值(x_train = [1,2,3,4,5,6], y_train = [1,3,5,7,9,11]
)的设定函数就是 y=2x-1 (w=2,b=-1)
对我们程序开始给的初始化的值 w=1.1 b=-2.1,是非常不靠谱的,我们看到 loss 尽然是122这么高。通过1000次训练,得到了相当大的矫正。
我想训练出来的模型准确率之所以这么高,一是因为我们给的训练数据比较少,而是因为训练数据给的很理想。
现实生活中的数据可比这复杂多了,当然我们也有更好的模型来训练它,这是后话了。
运行结果:
real vale: [-0.9999999 0.10000014 1.2000003 2.3000002 3.4 4.61 ]
curr loss: 121.132095337
train step(0) loss:107.545296
train step(100) loss:0.0296359
train step(200) loss:0.01862564
train step(300) loss:0.018511334
train step(400) loss:0.018509919
train step(500) loss:0.018509876
train step(600) loss:0.018509895
train step(700) loss:0.018509895
train step(800) loss:0.018509895
train step(900) loss:0.018509895
W: [1.97131],b: [-0.93244034],loss: 0.018509895
[array([1.97131], dtype=float32), array([-0.93244034], dtype=float32)]从 tensorboard 上来看,loss 矫正的速度还是挺快的,大概在第200步之后,模型就稳定了。
通过上面的案例,我们再回到文章开篇提出的问题。加入我们知道小明数次选择,假使小明我们的考虑的因素是固定不变的而且外部环境没有发生变化,下次要不要出门,我们就能求出概率啦。哈哈。。。