光线追踪-引擎
要说目前最热门的图形学话题,自然非实时光线追踪了莫属了。在GDC 2018上,微软率先为DX 12 API增加了光线追踪模块,并且将其命名为DirectX Raytracing (DXR);而NV则紧随其后发布了基于实时光线追踪的RTX技术;并且直接将显卡型号都从GTX改成了RTX系列。此后,AMD也正式宣布了自家的ProRender渲染引擎将支持实时光线追踪。 当然,硬件厂商都这样了,游戏引擎也不能掉链子,诸如EA 寒霜引擎、EA Seed、Unreal 引擎、3DMark、Unity 引擎已经宣布将会引入光线追踪。不过,乍一听看起来这些似乎距离我们还有些遥远,直到前两天NVIDIA发布了RTX 2080 Ti、RTX 2080、RTX 2070游戏显卡,明确表示从硬件级别支持光线追踪。
光线追踪的历史
其实光线追踪并不是近几年才有的概念,它的历史甚至可以追溯到上世纪70年代。Arthur Appel 于 1968 年提出将光线追踪算法应用于图片渲染的概念,那时还叫 ray casting,这也是后来光线追踪的基石。但一直等到 10 年后的 1979 年,Turner Whitted才继续在论文An Improved Illumination Model for Shaded Display中,具体解析如何捕捉反射、阴影和反射。在光线投射的基础上,加入光与物体表面的交互。
而在电影行业中,早就用上了我们提及的光线追踪,他们已经有相当成熟的解决方案,完全可以达到以假乱真的效果,你看看漫威的科幻大片,是不是给你一种异常真实的错觉?没错,这就是光线追踪的魅力。至于为什么电影行业能这样做,原因不外乎有两个:一是有时间,他们采用的离线光线追踪,是要慢慢一帧帧渲染出来;二是有钱,通常特效工作室会使用到NVIDIA所说的渲染农场,不是一台电脑在算,而是一个个渲染集群服务器在工作,算力是你机箱里的GTX 1080 Ti成千上万倍,因此它们可以这样玩。
早在上世纪60年代,美国科学家已经尝试将光线投射应用于军事领域的计算机图形生成。随着技术的成熟,很快应用于好莱坞电影及动漫制作。目前,绝大多数需要后期特效的好莱坞电影,除了风格化的类型之外,基本都使用了光线追踪技术。如下图《狮子王》利用光线追踪技术渲染的画面

光线特性
运用光线追踪技术,有以下渲染特性:
- 更精确的反射、折射和透射。
- 更准确的阴影。包括自阴影、软阴影、区域阴影、多光源阴影等。
- 更精准的全局光照。
- 更真实的环境光遮蔽(AO)
光线追踪技术可以精确地反映复杂的反射、折射、透射、阴影、全局光等物理特性。当然,光线追踪也不是万全的渲染技术,它有苛刻的硬件要求、有限度的渲染特性支持以及噪点干扰等负面特点。
光线追踪
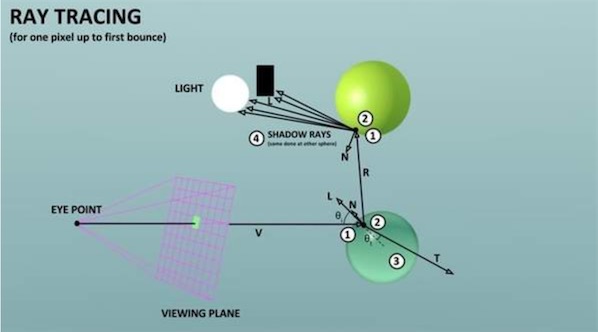
光线追踪主要思想是从视点向成像平面上的像素发射光线,找到阻挡光线传播的最近物体,如果交点表面为散射面,则计算光源直接照射该点产生的颜色;如果该交点表面为镜面或折射面,则继续向反射或折射方向跟踪另一条光线,如此往复循环,直到光线射出场景或者达到规定计算次数(还是为了节省资源)。这个方法被称之为经典光线跟踪方法或者递归式光线追踪方法。利用Compute Shader,屏幕的每个像素点向外释放一条射线来采样颜色,利用光线可逆的原则,每条光线根据碰撞到的物体进行反射,如此反复直到采样到天空盒(无限远)或者达到最大的反射次数。
我们将使用Unity引擎,C#结合compute shader实现光线追踪效果。本文中所有代码都上传到github上。
基本步骤
当渲染完成后,OnRenderImage方法会自动被Unity调用。代码里创建一张跟屏幕大小的RT 作为compute shader算法返回的结果。omputeShader中设置每个线程组为8x8,也就是每一组能处理8x8个像素, 线程组个数(高/8)*(宽/8),第三维度设置为1。添加RayTracingMaster组件到场景camera下, 这样OnRenderImage 才会被调到。
public class RayTracingMaster : MonoBehaviour
{
public ComputeShader RayTracingShader;
private RenderTexture _target;
private void OnRenderImage(RenderTexture source, RenderTexture destination) {
Render(destination);
}
private void Render(RenderTexture destination) {
InitRenderTexture();
RayTracingShader.SetTexture(0, "Result", _target);
int threadGroupsX = Mathf.CeilToInt(Screen.width / 8.0f);
int threadGroupsY = Mathf.CeilToInt(Screen.height / 8.0f);
RayTracingShader.Dispatch(0, threadGroupsX, threadGroupsY, 1);
Graphics.Blit(_target, destination);
}
private void InitRenderTexture() {
if (_target == null || _target.width != Screen.width
|| _target.height != Screen.height) {
if (_target != null)
_target.Release();
_target = new RenderTexture(Screen.width, Screen.height, 0,
RenderTextureFormat.ARGBFloat, RenderTextureReadWrite.Linear);
_target.enableRandomWrite = true;
_target.Create();
}
}
}
compute shader 需要传递一些camera的参数给compute shader, 主要是用来空间变换
- cameraToWorldMatrix 观察坐标系切换到世界坐标系
- projectionMatrix 观察坐标系转到投影坐标系 inverse是反过来,即投影坐标系变换到观察坐标系
traceShader.SetMatrix("_CameraToWorld", _camera.cameraToWorldMatrix);
traceShader.SetMatrix("_CameraInverseProjection", _camera.projectionMatrix.inverse);
在compute shader 部分, 定义个Ray的结构体来描述射线。 需要注意hlsl语法不像c#, 一个方法或者变量一定要先声明, 然后再去使用。 我们计算每条射线的起点和放线,然后输出对应的颜色, 对应的代码如下:
#pragma kernel CSMain
RWTexture2D<float4> Result;
float4x4 _CameraToWorld;
float4x4 _CameraInverseProjection;
struct Ray {
float3 origin;
float3 direction;
};
Ray CreateRay(float3 origin, float3 direction) {
Ray ray;
ray.origin = origin;
ray.direction = direction;
return ray;
}
Ray CreateCameraRay(float2 uv) {
// 观察空间到世界空间变换
float3 origin = mul(_CameraToWorld, float4(0.0f, 0.0f, 0.0f, 1.0f)).xyz;
// 投影空间变换到观察空间
float3 direction = mul(_CameraInverseProjection, float4(uv, 0.0f, 1.0f)).xyz;
// 变换到时间空间 w=0只变换方向
direction = mul(_CameraToWorld, float4(direction, 0.0f)).xyz;
direction = normalize(direction);
return CreateRay(origin, direction);
}
[numthreads(8,8,1)]
void CSMain (uint3 id : SV_DispatchThreadID) {
// 获取RT分辨率
uint width, height;
Result.GetDimensions(width, height);
// [0,1] 变换到 [-1,1]
float2 uv = float2((id.xy + float2(0.5f, 0.5f))/float2(width, height)*2.0f-1.0f);
Ray ray = CreateCameraRay(uv);
Result[id.xy] = float4(ray.direction * 0.5f + 0.5f, 1.0f);
}
这里我们导入天空盒是以texture2D而非texture3D的格式传入,所以我们需要把方向从笛卡尔坐标系转换为球坐标系,接着再除以π和π/2 把值映射至uv坐标的[0,1]范围内。直角坐标系(x,y,z)与球坐标系(r,θ,φ)的转换关系为:
想了解更多球面坐标系, 参考之前球谐光照的部分。
//因为我们天空盒导入的是2D的,所以要把方向转为球坐标系来采样
float theta = acos(ray.direction.y) / -PI;
float phi = atan2(ray.direction.x, -ray.direction.z) / -PI * 0.5f;
return _SkyboxTexture.SampleLevel(sampler_SkyboxTexture, float2(phi, theta), 0).rgb;
光线追踪流程
//光线进行7次反弹
float3 result=float3(0.0f,0.0f,0.0f);
for(int i=0;i<8;i++) {
RayHit hit=Trace(ray);
result+=ray.energy*Shade(ray,hit);
//光线能量耗尽直接退出循环
if(!any(ray.energy)) break;
}
首先是射线检测来寻找和场景中物体的碰撞情况,并将碰撞信息写入rayhit,接着在Shade方法内根据rayhit信息采样颜色,并且更新ray为碰撞点的入射光(原本是相对于碰撞点的出射光,我们的射线和光线是相反的)用于下一次的追踪。
按这个步骤循环进行多次从而形成完整的光线路径,当然不可能模拟无限反弹,我们这里限制最多7次
碰撞物:
也就是场景中的物体,我们先跳过网格,用相交性检测的方式来模拟圆和平面,如果射线和指定物体碰撞且距离最近,就将结果存入rayhit,共着色函数(Shade)使用。 这里使用的算法在文章的最后还有详细的推导。
//y=0的平面的射线相交检测
void IntersectGroundPlane(Ray ray,inout RayHit bestHit) {
float t=-ray.origin.y/ray.direction.y;
if(t>0&&t<bestHit.distance) {
bestHit.distance=t;
bestHit.position=ray.origin+t*ray.direction;
bestHit.normal=float3(0,1,0);
bestHit.albedo=float3(1.0f,1.0f,1.0f);
bestHit.specular=float3(0.2f,0.2f,0.2f);
}
}
//球的相交检测
void IntersectSphere(Ray ray, inout RayHit bestHit, Sphere sphere) {
float3 d = ray.origin - sphere.position;
float p1 = -dot(ray.direction, d);
float p2sqr = p1 * p1 - dot(d, d) + sphere.radius * sphere.radius;
if (p2sqr < 0) //不想交的情况
return;
float p2 = sqrt(p2sqr);
float t = p1 - p2 > 0 ? p1 - p2 : p1 + p2;
if (t > 0 && t < bestHit.distance) {
bestHit.distance = t;
bestHit.position = ray.origin + t * ray.direction;
bestHit.normal = normalize(bestHit.position - sphere.position);
bestHit.albedo=sphere.albedo;
bestHit.specular=sphere.specular;
}
}
着色:
采样颜色并且更新ray信息 这里有一个energy的概念,你可以把它想成光线的损耗度,因为物体是会吸收部分光线的,假设原本的光线强度为1,他碰撞到的第一个物体的specular0.6,物体吸收了0.4后反射的光线强度就变为0.6了(表现出来的就是物体的颜色),第二个Specular为0.8,那么就只剩下0.48,以此类推直到进入我们的眼睛。乘法顺序改变不会有影响,所以我们反着来的射线追踪也直接乘就好。
float3 Shade(inout Ray ray,RayHit hit) {
if(hit.distance<1.#INF) {
ray.origin=hit.position+hit.normal*0.001f;
ray.direction=reflect(ray.direction,hit.normal);
ray.energy*=hit.specular;
return float3(0.0f,0.0f,0.0f)
}else{
ray.energy=0;
//没有碰撞的物体就采样天空盒
//因为我们天空盒导入的是2D的,所以要把方向转为极坐标来采样
float theta = acos(ray.direction.y) / -PI;
float phi = atan2(ray.direction.x, -ray.direction.z) / -PI * 0.5f;
return _SkyboxTexture.SampleLevel(sampler_SkyboxTexture, float2(phi, theta), 0).rgb;
}
}
主光源:
前面我们采样的光源颜色全部来自天空盒,也就是环境光,现在我们加入主光源的影响, 这里我们添加albedo值,实现方法就是简单的兰伯特光照模型 直接返回。
return saturate(dot(hit.normal,_DirectionLight.xyz)*-1)*_DirectionLight.w*hit.albedo;
要注意的是现在我们有了两个获得光源的地方,所以得到的颜色综合了两者。
如图,黄色为直接光,蓝色为我们的追踪光线,所以我们可以理解为,光线追踪追踪的实际是物体的间接光,而每个物体还会有它的直接光,这解释了之前除了采样到天空盒,shade函数返回值都为0,而现在我们返回了直接光的光照值。
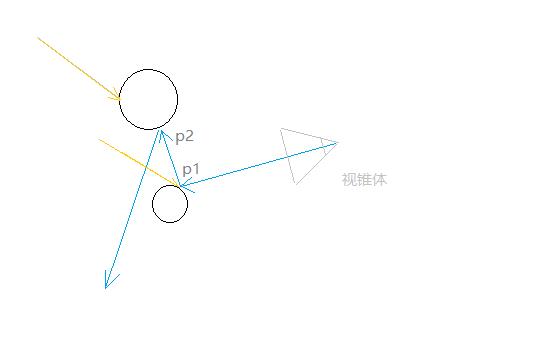
我们可以发现第二个碰撞点实际是在阴影下的,所以我们还需要检测阴影。要注意的是这里我们需要的是直射光反向的反射方向,不是我们的射线方向。
//阴影检测,向直射光的反方向进行射线检测,如果撞到了物体,就说明他在直射光的阴影之下,返回0
Ray shadowRay = CreateRay(hit.position + hit.normal * 0.001f, -1 * _DirectionLight.xyz);
RayHit shadowHit = Trace(shadowRay);
if (shadowHit.distance != 1.#INF)
抗锯齿:
因为我们是每个像素进行采样的,也就是说内容其实是不连续的,所以结果是会有很难看的锯齿, 解决办法就是每次采样,都对射线发射坐标进行轻微的偏移,然后获取采样的平均值。
//映射至uv的01范围内
float2 uv=float2((id.xy+_PixelOffset.xy)/float2(width,height)*2.0f-1.0f);
然后我们在新增一个pass,对每次采样进行平均。
Cull Off ZWrite Off ZTest Always
Blend SrcAlpha OneMinusSrcAlpha
Pass
{
CGPROGRAM
#pragma vertex vert
#pragma fragment frag
#pragma multi_compile_fog
#include "UnityCG.cginc"
struct appdata {
float4 vertex : POSITION;
float2 uv : TEXCOORD0;
};
struct v2f {
float2 uv : TEXCOORD0;
UNITY_FOG_COORDS(1)
float4 vertex : SV_POSITION;
};
sampler2D _MainTex;
float4 _MainTex_ST;
float _Sample;
v2f vert (appdata v) {
v2f o;
o.vertex = UnityObjectToClipPos(v.vertex);
o.uv = TRANSFORM_TEX(v.uv, _MainTex);
UNITY_TRANSFER_FOG(o,o.vertex);
return o;
}
float4 frag (v2f i) : SV_Target {
return float4(tex2D(_MainTex, i.uv).rgb, 1.0f / (_Sample + 1.0f));
}
ENDCG
}
这里之所以能够均值采样, 是因为每次都往颜色缓冲里写值,在写值的时候和颜色缓冲里的值进行Blend, 由于Blend方式是Blend SrcAlpha OneMinusSrcAlpha, 所以在_Sample递增的时候, 相当于与历史的值进行求平均。这样的求均值方式在后面的路径追踪算法里还会有别的用处。
路径追踪
我们假设每次光线都是表面法线进行的完美反射,所以他可以很好的展现光滑物体表面的反射效果。但是现实生活着并不是所有物体都是非常光滑的,这种方法无法展现物体之间相互作用的漫反射,还有物体的光泽。
渲染方程
$L_o(x,\vec{w_o})$:碰撞点X在w方向的出射光
$L_e(x,\vec{w_o} )$: 出射光的自发光贡献
$\int _\Omega …$: Ω=法线方向的半球面,这个积分的意思就是综合这个半球面所有可能方向的入射光对这个指定的出射光线的贡献。
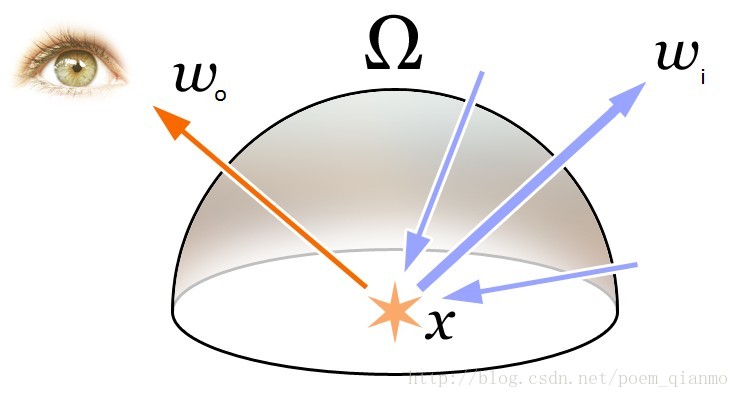
$f_r(x,\vec{w_i},\vec{w_o})$:双向反射分布函数BRDF
$\vec{w_i }\cdot \vec{n}$: 入射光和表面法线的夹角cos值,夹角越大,值越低,出射光强度越弱,因为夹角越大大,一束光线越容易分散
$L(x,\vec{w_i})$: 入射光,这个值就是前一个碰撞点用渲染方程得到的出射光,如此递归直到结束。
蒙特卡洛积分
我们无法明确的知道入射光来自哪些方向,所以我们使用蒙特卡洛方法在所有可能的方向中随机采样,我们采样的越多,越接近正确的结果。
这里我们先假设光线在半球面的各个方向的入射几率都是相同的,也就是说p(x_n)=\frac{1}{2\pi }。(单位半球的表面积为2π)。
先前的渲染公式就可以修改成如下:
上式$2\pi$是半球表面积, 式子左侧是漫反射Diffuse计算, 右侧是高光Specular求解。
前一章为了抗锯齿,我们使用addshader对多次采样进行平均取值,正好完成了公式中的这部分,但是因为OnRenderImage中的destination纹理精度为R8G8B8A8的类型,而我们希望的是RGBAfloat的精度,所以我们要再创建一个贴图用于来回倒,至于为什么要这样一个精度后面有提到。
又是上一条光线的递归结果(也就是代码中的energy),所以我们修改的就是绿色的这个部分。关于如何优雅计算BRDF, 采样方式 处理流程就是类似PBR对间接光的处理, 参照我之前的文章:基于图像的光照IBL。下面是一些实现的细节:
随机值
GPU里没有类似random()函数之类的算法, 需要自己去实现, 下面是网上的产生随机值算法。
float2 _Pixel;
float _Seed;
float rand()
{
float result = frac(sin(_Seed / 100.0f * dot(_Pixel, float2(12.9898f, 78.233f))) * 43758.5453f);
_Seed += 1.0f;
return result;
}
_Pixel直接在CSMain里初始化: _Pixel=id.xy, 所以每个像素都使用不同的随机值。 _Seed是c#侧传过来的初始值,这里当做随机种子使用。
漫反射
Lambert BRDF: $f_r(x, \, \vec \omega_{i}, \, \vec \omega_{o}) = \frac{k_d}{\pi}$, 其中$k_d$代表着材质的albeo
高光
这里使用的是brdf简化公式, $\alpha$代表着粗糙度:
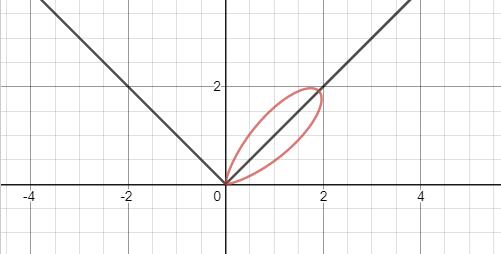
图为α=15,入射光为45度(左侧斜线)时的图像,红色是各个方向的出射光最终得到的值,可以看到出射光方向等于反射方向(右侧斜线)时值最大,约为$2\sqrt{2}$,一旦偏离这个方向,值就会迅速降低。

自发光
相当于新的光线并入这条光路,所以直接return自发光颜色
Mesh 碰撞检测
在计算机图形学中,网格由许多缓冲区定义,其中最重要的缓冲区是顶点缓冲区和索引缓冲区。顶点缓冲区是一个三维向量列表,描述每个顶点在对象空间中的位置(这意味着当您平移、旋转或缩放对象时,这些值不需要更改,而是使用矩阵乘法从对象空间动态地转换到世界空间)。索引缓冲区是指向顶点缓冲区的索引整数列表。每三个指数构成一个三角形。例如,如果索引缓冲区为[0,1,2,0,2,3],则有两个三角形:第一个三角形由顶点缓冲区中的第一、第二和第三个顶点组成,而第二个三角形由第一、第三和第四个顶点组成。因此,索引缓冲器还定义了上述的缠绕顺序。除了顶点和索引缓冲区之外,其他缓冲区还可以向每个顶点添加信息。最常见的附加缓冲区存储法线、纹理坐标(称为texcoords或简单的uv)和顶点颜色。
因此, 我们需要把游戏中需要渲染的mesh的顶点和索引告诉compute shader, 方式如下:
private void RebuildMeshObjectBuffers() {
if (!_meshObjectsNeedRebuilding) return;
_meshObjectsNeedRebuilding = false;
_currentSample = 0;
_meshObjects.Clear();
_vertices.Clear();
_indices.Clear();
// Loop over all objects and gather their data
foreach (RayTracingObject obj in _rayTracingObjects) {
Mesh mesh = obj.GetComponent<MeshFilter>().sharedMesh;
int firstVertex = _vertices.Count;
_vertices.AddRange(mesh.vertices);
int firstIndex = _indices.Count;
var indices = mesh.GetIndices(0);
_indices.AddRange(indices.Select(index => index + firstVertex));
_meshObjects.Add(new MeshObject() {
localToWorldMatrix = obj.transform.localToWorldMatrix,
indices_offset = firstIndex,
indices_count = indices.Length
});
}
CreateComputeBuffer(ref _meshObjectBuffer, _meshObjects, 72);
CreateComputeBuffer(ref _vertexBuffer, _vertices, 12);
CreateComputeBuffer(ref _indexBuffer, _indices, 4);
}
shader 中判断三角形是否与射线相交的算法, 在文章后面的部分会介绍推导, Mesh是由大量的三角形构成,我们遍历mesh里的每个三角形, 这里用来判断射线和Mesh相交。
void IntersectMeshObject(Ray ray, inout RayHit bestHit, MeshObject meshObject)
{
uint offset = meshObject.indices_offset;
uint count = offset + meshObject.indices_count;
for (uint i = offset; i < count; i += 3) {
float4x4 local2world = meshObject.localToWorldMatrix;
float3 v0 = (mul(local2world, float4(_Vertices[_Indices[i]], 1))).xyz;
float3 v1 = (mul(local2world, float4(_Vertices[_Indices[i + 1]], 1))).xyz;
float3 v2 = (mul(local2world, float4(_Vertices[_Indices[i + 2]], 1))).xyz;
float t, u, v;
if (IntersectTriangle_MT97(ray, v0, v1, v2, t, u, v)) {
if (t > 0 && t < bestHit.distance) {
bestHit.distance = t;
bestHit.position = ray.origin + t * ray.direction;
bestHit.normal = normalize(cross(v1 - v0, v2 - v0));
bestHit.albedo = 0.0f;
bestHit.specular = 0.65f;
bestHit.smoothness = 0.99f;
bestHit.emission = 0.0f;
}
}
}
}
不要使用任何过多的网格(超过几百个三角形)!我们的着色器缺少正确的优化,如果超出范围,每像素跟踪一个样本可能需要几秒钟甚至几分钟的时间。结果是你的GPU驱动程序将被系统杀死,Unity可能会崩溃,你的机器需要重新启动。最终运行的效果如下图:

射线相交检测算法
1. 射线与平面相交
射线: $R(t) = O + tD$(O原点, D方向, t距离)
设O的坐标(x, y, z) 方向使用向量D=(x’, y’, z’)
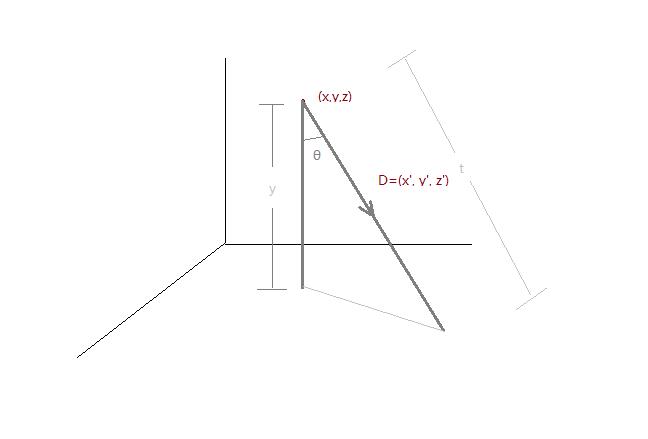
图中可以看到射线起点到地平面(y=0, x-z 平面), 即射线起点纵坐标y除上余弦值。
把上式$\cos\theta$代入分母:
所以代码里实现如下:
bool IntersectPlane(Ray ray) {
t = -ray.origin.y / ray.direction.y;
return true;
}
2. 射线与球相交
射线:$R(t)=O+tD$
圆:pos+radius
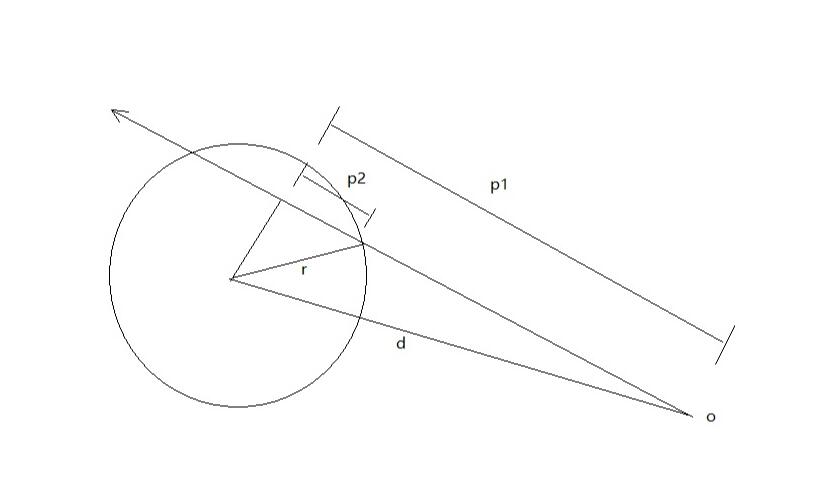
得到向量 $d= pos-O$
点乘单位向量得到投影 $P_1=d\cdot D$
两次勾股定律得到p2平方 $(P_2)^2=r^2-(d^2-p_1^2)$
<0无解 =0 一解 >0 两解 $t=P_1\pm P_2$
如果有两个解,就选距离最短的那个解,看图可以知道最短的就是进入圆的点,圆的是退出圆。
bool IntersectSphere(Ray ray, float3 position,float radius,inout float t) {
float3 d = ray.origin - position;
float p1 = -dot(ray.direction, d);
float p2sqr = p1 * p1 - dot(d, d) +radius*radius;
if (p2sqr < 0)//不存在解也就是不相交
return false;
float p2 = sqrt(p2sqr);
t = p1 - p2 > 0 ? p1 - p2 : p1 + p2;//优先选近的那个点,除非近的点在后头
return true;
}
3. 射线与三角形相交
射线:$R(t)=O+tD$
射线,一个点从起点o开始,沿着方向D移动任意长度,得到终点R,根据t值的不同,得到的R值也不同,所有这些不同的R值便构成了整条射线,比如下面的射线,起点是P0,方向是u,p0 + tu也就构成了整条射线。
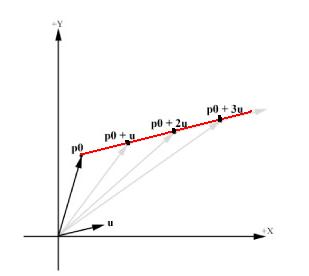
三角形的参数方程如下,其中V0,V1和V2是三角形的三个点,u, v是V1和V2的权重,1-u-v是V0的权重,并且满足u>=0, v >= 0,u+v<=1。
确切的说,上面的方程是三角形及其内部所有点的方程,因为三角形内任意一点都可以理解为从顶点V0开始,沿着边V0V1移动一段距离,然后再沿着边V0V2移动一段距离,然后求他们的和向量。至于移动多大距离,就是由参数u和v控制的。
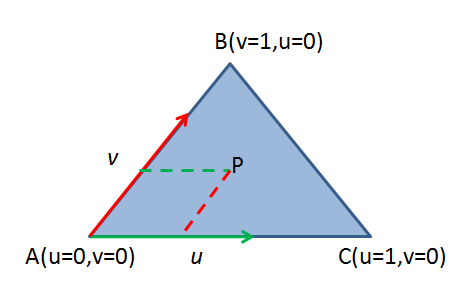
于是,求射线与三角形的交点也就变成了解下面这个方程-其中t,u,v是未知数,其他都是已知的
移项并整理,将t,u,v提取出来作为未知数,得到下面的线性方程组
现在开始解这个方程组,这里要用到两个知识点,一是克莱姆法则,二是向量的混合积。
令E1=V1−V0,E2=V2−V0,T=O−V0上式可以改写成:
根据克莱姆法则,可得到t,u,v的解为:
根据混合积公式:
上式改写为:
令$P=D×E_2,Q=T×E_1$,得到最终的公式:
之所以提炼出P和Q是为了避免重复计算。
//三角形的相交性检测 双面 uvw 重心坐标 w=1-u-v t=距离
static const float EPSILON = 1e-8;
bool IntersectTriangle_01(Ray ray, float3 vert0, float3 vert1, float3 vert2,
inout float t, inout float u, inout float v,inout float toward) {
//E1 E2
float3 edge1 = vert1 - vert0;
float3 edge2 = vert2 - vert0;
//P=DxE2
float3 pvec = cross(ray.direction, edge2);
float det = dot(edge1, pvec);
//背面det<0 正面>0 在三角形内=0
if (det < EPSILON&&det >-EPSILON) return false;
toward=sign(det);
// 1/(DxE2)·E1
float inv_det = 1.0f / det;
//T
float3 tvec = ray.origin - vert0;
//u=invdet *(P·T)
u = dot(tvec, pvec) * inv_det;
//如果三角形内的点,重心坐标一定在[0,1]
if (u < 0.0 || u > 1.0f) return false;
//Q=TxE1
float3 qvec = cross(tvec, edge1);
//v=invdet*(Q·D)
v = dot(ray.direction, qvec) * inv_det;
if (v < 0.0 || u + v > 1.0f) return false;
//t=Q·E2
t = dot(edge2, qvec) * inv_det;
return true;
}
4. 射线与立方盒相交
主要是BVH算法会用到, 下面一节会用到。
默认在对象空间计算,需要将光线转至立方盒的对象空间
射线:$R(t)=O+tD (O原点,D方向,t距离)$
立方体:$x=0;y=0;z=0;x=r_x;y=r_y;z=r_z$(由六个面组成)
推导过程:
① 寻找可能正面相交的平面(最多三个)
通过光线方向的三个分量判断各自两个面的相交情况,以x轴为例:
$D_x>0$:光线与平面x=0相交
$D_x<0$:光线与平面$x=r_x$相交
$D_x=0$ :两个面都不相交
② 计算与平面的焦点,得到最近的相交点(在矩形内部)
将R(t)带入各个面,以$x=r_x$为例
可以确定焦点的x值为$r_x$,带入R(t)推出t值
然后根据t得到交点的另外两个分量
如果该交点另外两个分量满足下面两个条件,则该点就是最近的相交点,不用再考虑其他平面了。
代码:
#define ISPOINT(name,c1,c2) name.c1>=0&&name.c1<=cubeSize.c1&& name.c2>=0&&name.c2<=cubeSize.c2
//立方体 对象空间
bool IntersectCube(Ray ray,float3 cubeSize,inout float t,inout float3 normal){
//1.用矩阵将射线转为立方体的对象空间,略 后面的法线也应该转回世界空间
float3 rayOri=ray.origin;
float3 rayDir=ray.direction;
float3 pos;
//x轴两个面
if(rayDir.x<0){
t=(cubeSize.x-rayOri.x)/rayDir.x;
pos=rayOri+t*rayDir;
if(ISPOINT(pos,y,z)){
normal=float3(1,0,0);
return true;
}
}
else if(rayDir.x>0){
t=-rayOri.x/rayDir.x;
pos=rayOri+t*rayDir;
if(ISPOINT(pos,y,z)){
normal=float3(-1,0,0);
return true;
}
}
//y轴两个面
if(rayDir.y<0){
t=(cubeSize.y-rayOri.y)/rayDir.y;
pos=rayOri+t*rayDir;
if(ISPOINT(pos,x,z)){
normal=float3(0,1,0);
return true;
}
}
else if(rayDir.y>0){
t=-rayOri.y/rayDir.y;
pos=rayOri+t*rayDir;
if(ISPOINT(pos,x,z)){
normal=float3(0,-1,0);
return true;
}
}
//z轴两个面
if(rayDir.z<0){
t=(cubeSize.z-rayOri.z)/rayDir.z;
pos=rayOri+t*rayDir;
if(ISPOINT(pos,x,y)){
normal=float3(0,0,1);
return true;
}
}
else if(rayDir.z>0){
t=-rayOri.z/rayDir.z;
pos=rayOri+t*rayDir;
if(ISPOINT(pos,x,y)){
normal=float3(0,0,-1);
return true;
}
}
return false;
}