TensorFlow-搭建 CNN 网络
人工神经网络是由大量处理单元互联组成的非线性、自适应信息处理系统。它是在现代神经科学研究成果的基础上提出的,试图通过模拟大脑神经网络处理、记忆信息的方式进行信息处理。
CNN(Convolutional Neural Network)——卷积神经网络,人工神经网络(Neural Network,NN)的一种,其它还有RNN、DNN等类型,而CNN就是利用卷积进行滤波的神经网络。换句话说,CNN就是卷积加神经网络。
卷积神经网络是一种特殊的深层的神经网络模型,它的特殊性体现在两个方面,一方面它的神经元间的连接是非全连接的, 另一方面同一层中某些神经元之间的连接的权重是共享的(即相同的)。它的非全连接和权值共享的网络结构使之更类似于生物 神经网络,降低了网络模型的复杂度(对于很难学习的深层结构来说,这是非常重要的),减少了权值的数量。现在 以CNN 神经网络模型的主要用来图像归类、语音识别。
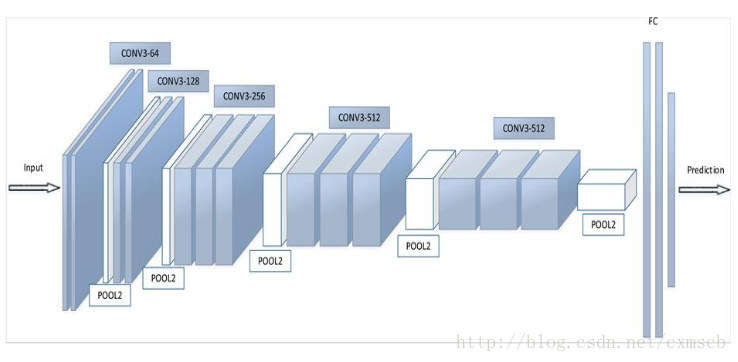
主流的CNN 神经网络主要包含以下几个步骤: 输入(in)->卷积(conv2d)->池化(pooling)->全连接(Fully Connect)->归类(softmax)->输出(out)
下面以 Python 语言展示cnn 的 Graph 生成过程。
- 定义 W 权重和 biases
def var_weight(shape):
# tf.truncated_normal(shape, mean, stddev)
# shape表示生成张量的维度,mean是均值,stddev是标准差
return tf.Variable(tf.truncated_normal(shape,stddev=0.1))
def var_bias(shape):
return tf.Variable(tf.constant(0.1,shape=shape))卷积 conv2d 与池化 pooling 操作
首先,关于什么是卷积,文章(3)有一牛人用一句话总结得很好:卷积就是带权的积分,看下面的一维卷积公式:
函数值与权值的乘积相加即可得到卷积值c(x),换句话说,我们对函数值的加权叠加,即可得到x处的卷积值。CNN利用的是多维卷积,但原理一样,不多说了,同时建议不要过多纠缠这个概念,理解就好,以后若作科研再作深入了解。对于图像处理,CNN会对输入图像矩阵化,然后从矩阵第一个元素开始逐一进行卷积运算。
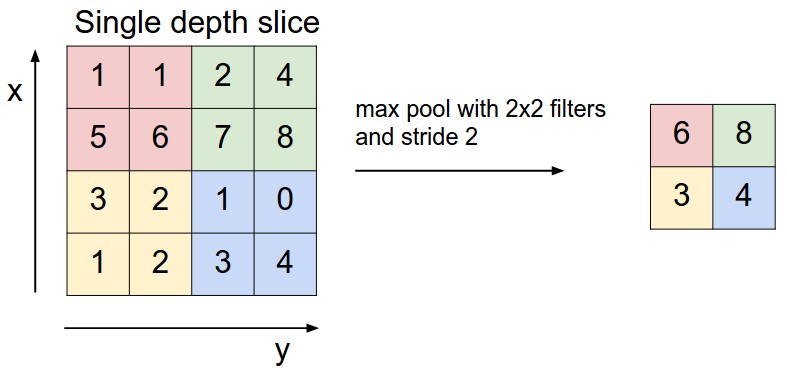
池化层存在的目的是缩小输入的特征图,简化网络计算复杂度;同时进行特征压缩,突出主要特征。简言之,即取区域平均或最大,如下图所示
# 卷积操作
def conv2d(x,W):
"""
卷积遍历各方向步数为1,SAME:边缘外自动补0,遍历相乘
"""
return tf.nn.conv2d(x,W,[1,1,1,1],padding="SAME")
# 池化操作
def maxpool(x):
"""
图像长宽压缩,过滤无用的信息
池化层采用kernel大小为2*2,步数也为2,周围补0,取最大值。数据量缩小了4倍
"""
return tf.nn.max_pool(x,ksize=[1,2,2,1],strides=[1,2,2,1],padding='SAME')
# padding='SAME' 表示输出大小不会发生改变,filter 以0填充
# padding='VILID' 信息会有损 一般在池化pooling才会改变大小
# 定义模型输入 这里从 MNIST 测试数据获取
xs=tf.placeholder(tf.float32,[None,784])/255
ys=tf.placeholder(tf.float32,[None,10])
keep_prob = tf.placeholder(tf.float32)
x_image = tf.reshape(xs, [-1, 28, 28, 1])第一层神经网络 以5x5的 过滤器(filter)
输出深度为32的卷积池化操作, 卷积之后得到的大小是28x28x32,池化之后得到的大小是14x14x32
"""
第一二参数值得卷积核尺寸大小,即patch,第三个参数是图像通道数,第四个参数是卷积核的数目,代表会出现多少个卷积特征图像
"""
W_conv1 = var_weight([5,5,1,32])
b_conv1 = var_bias([32])
# 图片乘以卷积核,并加上偏执量,卷积结果28x28x32
h_conv1 = tf.nn.relu(conv2d(x_image, W_conv1) + b_conv1)
h_pool1 = maxpool(h_conv1) # output size 14x14x32激活函数层:它的作用前面已经说了,这里讲一下代码中采用的relu(Rectified Linear Units,修正线性单元)函数,它的数学形式如下:
ƒ(x) = max(0, x)
这个函数非常简单,其输出一目了然,小于0的输入,输出全部为0,大于0的则输入与输出相等。该函数的优点是收敛速度快,除了它,keras库还支持其它几种激活函数,如下:
softplus
softsign
tanh
sigmoid
hard_sigmoid
linear它们的函数式、优缺点度娘会告诉你,不多说。对于不同的需求,我们可以选择不同的激活函数,这也是模型训练可调整的一部分,运用之妙,存乎一心,请自忖之。
第二层继续卷积池化操作
使图像继续长宽变小深度加厚,第二层输出的大小事7x7x64
## conv2 layer ##
W_conv2 = var_weight([5,5, 32, 64]) # patch 5x5, in size 32, out size 64
b_conv2 = var_bias([64])
h_conv2 = tf.nn.relu(conv2d(h_pool1, W_conv2) + b_conv2) # output size 14x14x64
h_pool2 = max_pool(h_conv2) # output size 7x7x64第三层 全连接层(dense layer)
全连接层的作用就是用于分类或回归,对于我们来说就是分类。keras将全连接层定义为Dense层,其含义就是这里的神经元连接非常“稠密”。我们通过Dense()函数定义全连接层。这个函数的一个必填参数就是神经元个数,其实就是指定该层有多少个输出。在我们的代码中,第一个全连接层(#14 Dense层)指定了512个神经元,也就是保留了512个特征输出到下一层。这个参数可以根据实际训练情况进行调整,依然是没有可参考的调整标准,自调之。
W_fc1 = var_weight([7*7*64, 1024])
b_fc1 = var_bias([1024])
# [n_samples, 7, 7, 64] ->> [n_samples, 7*7*64]
h_pool2_flat = tf.reshape(h_pool2, [-1, 7*7*64])
h_fc1 = tf.nn.relu(tf.matmul(h_pool2_flat, W_fc1) + b_fc1)
h_fc1_drop = tf.nn.dropout(h_fc1, keep_prob)第四层 正则化-归类
数据集先浮点后归一化的目的是提升网络收敛速度,减少训练时间,同时适应值域在(0,1)之间的激活函数,增大区分度。其实归一化有一个特别重要的原因是确保特征值权重一致。举个例子,我们使用mse这样的均方误差函数时,大的特征数值比如(5000-1000)2与小的特征值(3-1)2相加再求平均得到的误差值,显然大值对误差值的影响最大,但大部分情况下,特征值的权重应该是一样的,只是因为单位不同才导致数值相差甚大。因此,我们提前对特征数据做归一化处理,以解决此类问题。关于归一化的详细介绍有兴趣的请参考如下链接:深入理解CNN细节之数据预处理
## fc2 layer ##
W_fc2 = var_weight([1024, 10])
b_fc2 = var_bias([10])
prediction = tf.nn.softmax(tf.matmul(h_fc1_drop, W_fc2) + b_fc2)-
计算结果
用交叉熵计算损失,优化器迭代,每隔50步打印准确度
# the error between prediction and real data
# 定义交叉熵为loss函数
cross_entropy = tf.reduce_mean(-tf.reduce_sum(ys * tf.log(prediction),reduction_indices=[1])) # loss
# 调用优化器优化,其实就是通过喂数据争取cross_entropy最小化
train_step = tf.train.AdamOptimizer(1e-4).minimize(cross_entropy)
with tf.Session() as sess:
init = tf.global_variables_initializer()
sess.run(init)
for i in range(1000):
batch_xs, batch_ys = mnist.train.next_batch(100)
sess.run(train_step, feed_dict={xs: batch_xs, ys: batch_ys, keep_prob: 0.5})
if i % 50 == 0:
print(compute_accuracy(mnist.test.images[:1000], mnist.test.labels[:1000]))运行结果:
Extracting MNIST_data/train-images-idx3-ubyte.gz
Extracting MNIST_data/train-labels-idx1-ubyte.gz
Extracting MNIST_data/t10k-images-idx3-ubyte.gz
Extracting MNIST_data/t10k-labels-idx1-ubyte.gz
2018-03-12 13:40:29.201888: I tensorflow/core/platform/cpu_feature_guard.cc:137] Your CPU supports instructions that this TensorFlow binary was not compiled to use: SSE4.2 AVX AVX2 FMA
0.054
0.767
0.866
0.895
0.905
0.925
0.928
0.931
0.938
0.943
0.943
0.951
0.951
0.961
0.962
0.96
0.967
0.963
0.967
0.966
[Finished in 218.8s]从最终结果可以看出,运行的准确率可以达到96.6%,注意编译运行的时候负载特别高
通过上面的案例,我们再回到文章开篇提出的问题。加入我们知道小明数次选择,假使小明我们的考虑的因素是固定不变的而且外部环境没有发生变化,下次要不要出门,我们就能求出概率啦。哈哈。。。